- 余弦定理的应用
- 共29题
1
题型:简答题
|
19.如图,在

(1)若AD=2,
(2)若AB=AD,试求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
正弦定理余弦定理的应用三角形中的几何计算解三角形的实际应用
1
题型:填空题
|
14.在△ABC中,D为边BC上一点,BD=



正确答案
60°
解析
解析已在路上飞奔,马上就到!
知识点
余弦定理的应用
1
题型:简答题
|
16.已知


(1)求角C的大小;
(2)若
正确答案
(1)C= 
(2)a=2,b=4或a=4,b=2
解析
解析已在路上飞奔,马上就到!
知识点
正弦定理的应用余弦定理的应用平面向量共线(平行)的坐标表示
1
题型:简答题
|
17.在△ABC中,B=

正确答案
△ABC是等边三角形.
解析
直接按照已知条件转换成关于角C有关的表达式,最后将式子化简后来求.
在△ABC中,根据
得
同理BC=2sinA,因此AB+BC=2sinC+2sinA
=

因此AB+BC的最大值为

考查方向
本题考查了正弦定理与三角恒定变换.
解题思路
根据正弦定理将边转化为只与角C有关的式子,然后用化简后用辅助角公式合二为一,最后求出最大值及取到最大值的角C,从而判断出此时三角形的形状。
易错点
利用辅助角公式进行合二为一。
知识点
三角函数中的恒等变换应用余弦定理的应用
1
题型:简答题
|
17.在

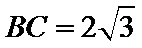
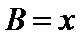

(1)求函数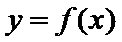
(2)求
正确答案
(1)
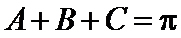
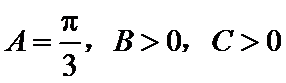
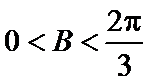
应用正弦定理,知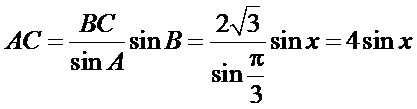

因为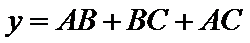
所以
(2)因为

所以,当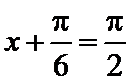
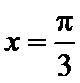
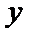
解析
解析已在路上飞奔,马上就到!
知识点
函数解析式的求解及常用方法余弦定理的应用
下一知识点 : 三角形中的几何计算
扫码查看完整答案与解析