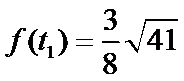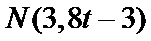- 余弦定理的应用
- 共29题
1
题型:
单选题
|
11.平面



正确答案
A
知识点
余弦定理的应用异面直线及其所成的角
1
题型:填空题
|
15.△ABC的内角A,B,C的对边分别为a,b,c,若

正确答案
知识点
正弦定理的应用余弦定理的应用
1
题型:简答题
|
18.
在△ABC中,角A,B,C所对的边分别是a,b,c,且
(I)证明:sinAsinB=sinC;
(II)若
正确答案
知识点
求函数y=Asin(ωx+φ)的解析式函数y=Asin(ωx+φ)的应用正弦定理的应用余弦定理的应用
1
题型:简答题
|
17.在



(1)求
(2)若


正确答案
(1)
解析
试题分析:本题属于正余弦定理及三角形的面积公式的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
(Ⅰ)由正弦定理,可得
∴
∴
∴

(Ⅱ)由已知

由余弦定理
∴
∴

∴

考查方向
本题考查了正余弦定理的综合应用、不等式等知识点。
解题思路
(1)直接利用正弦定理化边为角,进而求出角C的余弦值,从而求出C;
(2)利用三角形的面积公式及均值不等式即可求出c的最小值.
易错点
相关知识点不熟容易处错。
知识点
余弦定理的应用
1
题型:简答题
|
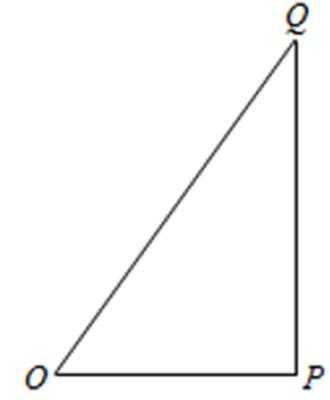
21.如图,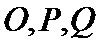
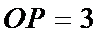
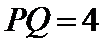
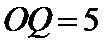
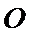
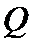
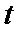
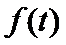
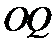
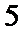
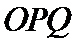
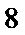
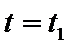
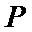
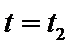

(1)求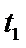
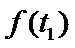
(2)已知警员的对讲机的有效通话距离是3千米,当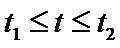
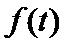
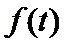
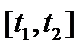
正确答案
(1)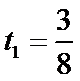
(2)见解析
解析
(1)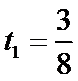
设乙到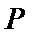
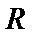
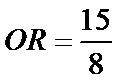
在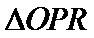
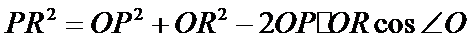
所以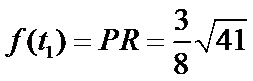
(2)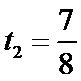
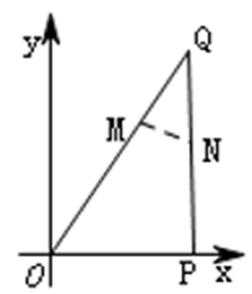
如图建立平面直角坐标系,
设经过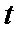
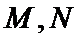
当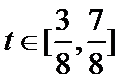
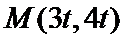
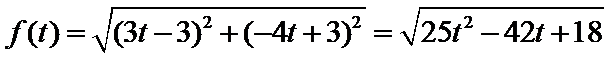
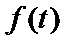
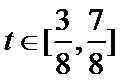
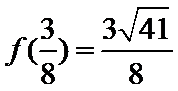
知识点
余弦定理的应用解三角形的实际应用
下一知识点 : 三角形中的几何计算
扫码查看完整答案与解析