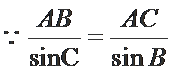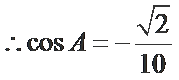- 余弦定理的应用
- 共29题
在△ABC中,角A,B,C所对的边分别是a,b,c,且
(I)证明:sinAsinB=sinC;
(II)若
正确答案
(Ⅰ)根据正弦定理,可设
则a=ksin A,b=ksin B,c=ksinC.
代入

sin A sin B=sin Acos B=sin (A+B).
在△ABC中,由A+B+C=π,有sin (A+B)=sin (π–C)=sin C,
所以sin A sin B=sin C.
(Ⅱ)由已知,b2+c2–a2=

所以sin A=
由(Ⅰ),sin Asin B=sin Acos B +cos Asin B,
所以


故tan B=
知识点
9.在△ABC中 ,B=
正确答案
知识点
在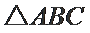
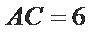

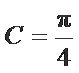
15.求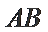
16. 求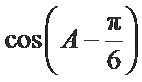
正确答案

解析
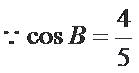

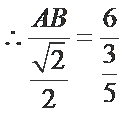
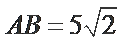
考查方向
解题思路
易错点
公式应用,公式变形。
正确答案

解析
又
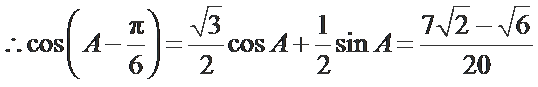
考查方向
解题思路
易错点
公式应用,公式变形。
9.已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而
形成的曲面所围成的几何体的体积为( )
正确答案
解析
由题意知,该等腰直角三角形的斜边长为2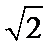
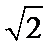

考查方向
解题思路
理解所得旋转体的几何特征,确定得到计
易错点
旋转体的几何特征的理解
知识点
已知函数
17.当

18.若




正确答案
(1)
解析
(1)



考查方向
解题思路
1。第(1)问先化简函数为一个角的一个三角函数,然后求其值域;
易错点
1.第(1)问直接将区间的端点带入函数导致值域出错;
正确答案
(2)
解析
(2)∵由题意可得

化简可得:





考查方向
解题思路
2.先由


易错点
2.第(2)问
13.设


正确答案
4
解析
由





正弦定理与余弦定理.
考查方向
解题思路
本题考查正弦定理与余弦定理的应用,先由正弦定理将
易错点
注意运算的准确性及最后结果还需开方.
知识点
已知向量

17.若

18.在




正确答案
解析

得
即


考查方向
解题思路
先通过向量垂直,得到三角关系,利用辅助角公式得到三角函数的解析式y=sin(x-



易错点
向量的坐标运算,三角函数的恒等变换
正确答案
(0,
解析
由

∴







考查方向
解题思路
将边用正弦定理进行转化,得到cosA=


易错点
向量的坐标运算,三角函数的恒等变换
5.在



正确答案
解析
因为
所以,


故选:C
考查方向
解题思路
由条件利用正弦定理化简
易错点
本题在利用正弦定理化简
知识点
15.在





正确答案
解析
由

考查方向
本题考查解三角形和三角函数知识。
解题思路
由已知确定a,c的两个方程可解得。
易错点
求解方向不明,无法借助所学知识转化,或者运算出错。
教师点评
本题考查了正弦定理,余弦定理,平方关系等知识,在近几年的各省高考题出现的频率较高,常与三角恒等变换等知识点交汇命题。
知识点
扫码查看完整答案与解析