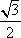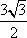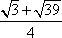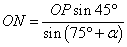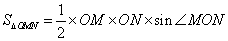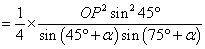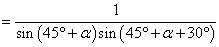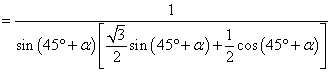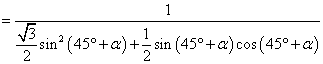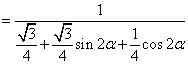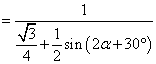- 三角形中的几何计算
- 共63题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
在△ABC中,AC=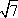
正确答案
解析
设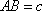
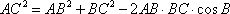
即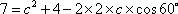
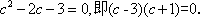
设BC边上的高等于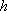
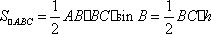
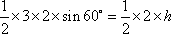
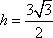
知识点
如图,在等腰直角三角形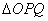
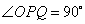
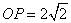
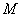

(1)若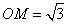

(2)若点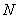
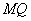
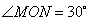
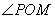

正确答案
见解析
解析
本小题主要考查解三角形、同角三角函数的基本关系、两角和与差的三角函数等基础知识,考查推理论证能力、抽象概括能力、运算求解能力,考查函数与方程思想、数形结合思想、化归与转化思想,满分12分。
(1)在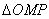
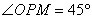

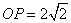
由余弦定理得,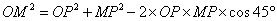
得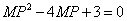
解得
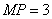
(2)设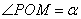
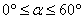
在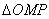
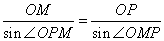
所以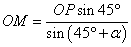
同理
故
因为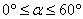
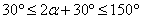
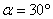
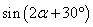
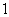
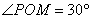


知识点
已知





正确答案
解析
方程化为
知识点
在腰长为2的等腰直角三角形内任取一点,使得该点到此三角形的直角顶点的距离不大于1的概率是( )
正确答案
解析
略
知识点
设一直角三角形的两条直角边长均是区间

正确答案
解析
设两条直角边长为
知识点
在底部周长
正确答案
24
解析
从图中读出底部周长在




知识点
△ABC中,
正确答案
解析
略
知识点
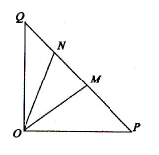
如图,
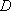


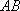
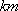
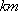
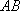

(1)某移动公司将在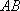
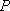
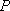
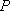

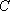



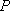
(2)环保部门将在
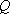
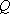
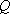

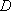

正确答案
(1)点
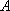
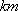
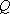
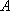
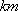
解析
(1)设
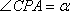
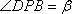
依题意有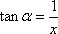
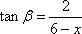
由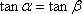
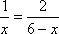
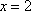

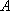
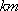
(2)设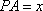
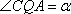

依题意有
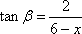
令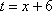
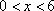
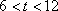
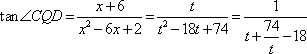
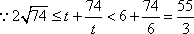
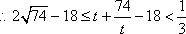
当
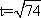
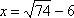
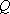
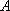
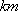
知识点
已知点O(0,0),A(0,b),B(a,a3),若△OAB为直角三角形,则必有( )。
正确答案
解析
若∠OBA为直角,则
即a2+(a3-b)·a3=0,
又a≠0,故
若∠OAB为直角时,
若∠AOB为直角,则不可能,所以b-a3-
知识点
扫码查看完整答案与解析