- 离散型随机变量及其分布列、均值与方差
- 共180题
18. 实验中学的三名学生甲、乙、丙参加某大学的自主招生考核测试,在本次考核中只有合格和优秀两个等次,若考核为合格,则授予10分降分资格;考核为优秀,授予20分降分资格。假设甲、乙、丙考核为优秀的概率分别为


(1)求在这次考核中,甲、乙、丙三名同学中至少有一名考核为优秀的概率;
(2)记在这次考核中甲、乙、丙三名同学所得的降分之和为随机变量
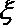
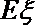
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.公安部最新修订的《机动车驾驶证申领和使用规定》于2013年1月1日起正式实施,新规实施后,获取驾照要经过三个科目的考试,先考科目一(理论一),科目一过关后才能再考科目二(桩考和路考),科目二过关后还要考科目三(理论二).只有三个科目都过关后才能拿到驾驶证.某驾校现有100名新学员,第一批参加考试的20人各科目通过的人数情况如下表:
请你根据表中的数据:
(Ⅰ)估计该驾校这100名新学员有多少人一次性(不补考)获取驾驶证;
(Ⅱ)第一批参加考试的20人中某一学员已经通过科目一的考试,求他能通过科目二却不能通过科目三的概率;
(Ⅲ)该驾校为调动教官的工作积极性,规定若所教学员每通过一个科目的考试,则学校奖励教官100元.现从这20人中随机抽取1人,记X为学校因为该学员而奖励教官的金额数,求X的数学期望.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.成都市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰。若现有500人参加测试,学生成绩的频率分布直方图如下:
(1)求获得参赛资格的人数;
(2)根据频率直方图,估算这500名学生测试的平均成绩;
(3)若知识竞赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛,已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 甲、乙两班参加数学知识竞赛,每班出3人组成代表队,每人一道必答题,答对为本队得1分,答错或不答得0分,假如甲队每人答对的概率均为




(Ⅰ)求随机变量

(Ⅱ)用A表示事件“甲、乙两队得分和为3”,B表示事件“甲队得分大于乙队得分”,求P(AB)
正确答案
解:(Ⅰ)
而P(






因而

(Ⅱ)P(AB)=
解析
解析已在路上飞奔,马上就到!
知识点
7.一盒中有


那么抽取次数

正确答案

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析








