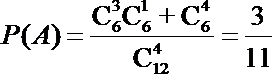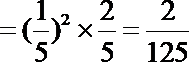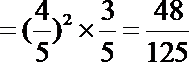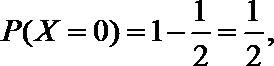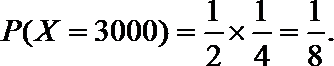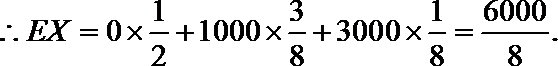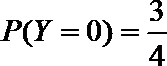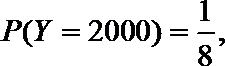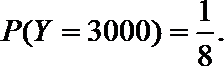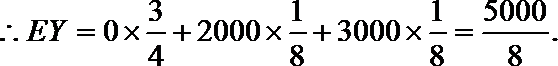- 离散型随机变量及其分布列、均值与方差
- 共180题
19.英语老师要求学生从星期一到星期四每天学习3个英语单词;每周五对一周内所学单词随机抽取若干个进行检测(一周所学的单词每个被抽到的可能性相同)
(1)英语老师随机抽了4个单词进行检测,求至少有3个是后两天学习过的单词的概率;
(2)某学生对后两天所学过的单词每个能默写对的概率为

正确答案
(1)设英语老师抽到的4个单词中,至少含有3个后两天学过的事件为A,则由题意可得
(2)由题意可得ξ可取0,1,2,3,则有P(ξ=0)
P(ξ=1)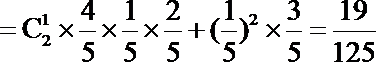
P(ξ=2) 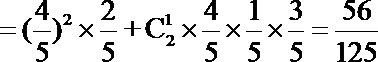
P(ξ=3)
所以ξ的分布列为:
故Eξ=0×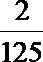
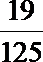
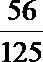
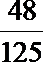
解析
解析已在路上飞奔,马上就到!
知识点
15.某地区为某类人员免费提供财会和计算机培训,参加培训者可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有





正确答案
2.7
解析
解析已在路上飞奔,马上就到!
知识点
19.某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的长势情况,从两块地各随机抽取了10株树苗,分别测出它们的高度如下(单位:cm)
甲:19 20 21 23 25 29 32 33 37 41
乙:10 26 30 30 34 37 44 46 46 47
(1)用茎叶图表示上述两组数据,并分别求两块地抽取树苗的高度的平均数和中位数;
(2)绿化部门分配这


(3)现苗圃基地将甲、乙两块地的树苗合在一起,按高度分成一、二两个等级,每个等级按不同的价格出售.某市绿化部门下属的2个单位计划购买甲、乙两地种植的树苗.已知每个单位购买每个等级树苗所需费用均为5万元,且每个单位对每个等级树苗买和不买的可能性各占一半,求该市绿化部门此次采购所需资金总额
正确答案
(1)画出茎叶图如下:
①甲地树苗高度的平均数为

②甲地树苗高度的中位数为


(2)都来自乙苗圃的概率为
(3)






∴
∴
∴该市绿化部门此次采购的资金总额
解析
解析已在路上飞奔,马上就到!
知识点
19.设计某项工程,需要等可能地从4个向量a=(2,3)、b=(1,5)、c=(4,3)、d=(8,1)中任选两个来计算数量积,若所得数量积为随机变量ξ.
(1)求随机变量ξ≤19的概率;
(2)求随机变量ξ的分布列和期望E(ξ).
正确答案
(1)
a·b=2×1+3×5=17,
a·c=2×4+3×3=17,
a·d=2×8+3×1=19,
b·c=1×4+5×3=19
b·d=1×8+5×1=13,
c·d=4×8+3×1=35
P(ξ≤19)=P(ξ=19)+P(ξ=17)+P(ξ=13)=
∴数量积ξ≤19的概率为
(2)数量积ξ可能取值为13,17,19,35,
P(ξ=13)=

P(ξ=19)=
数量积ξ的分布列为
数量积ξ的期望E(ξ)=
解析
解析已在路上飞奔,马上就到!
知识点
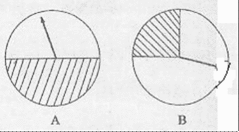
16.如图,两个圆形转盘A,B,每个转盘阴影部分各占转盘面积的

(1)记先转A转盘最终所得积分为随机量X,则X的取值分别是多少?
(2)如果你参加此活动,为了赢得更多的积分,你将选择先转哪个转盘?请说明理由。
正确答案
(1)X的取值分别是:0分,1000分,3000分
(2)由已知得,转动A盘得到积分的概率为
转动B盘得到积分的概率为
设先转A盘所得的积分为X分,先转B盘所得的积分为Y分,则有
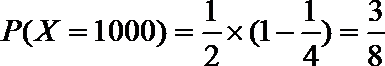
同理:
故先转A盘时,赢得积分平均水平较高。
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析