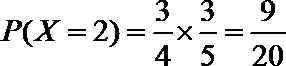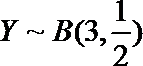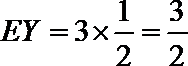- 离散型随机变量及其分布列、均值与方差
- 共180题
19.乒乓球台面被球网分隔成甲、乙两部分,如图,甲上有两个不相交的区域A,B,乙被划分为两个不相交的区域C,D.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在C上记3分,在D上记1分,其他情况记0分.对落点在A上的来球,队员小明回球的落点在C上的概率为,在D上的概率为;对落点在B上的来球,小明回球的落点在C上的概率为,在D上的概率为.假设共有两次来球且落在A,B上各一次,小明的两次回球互不影响.求:
(1)小明两次回球的落点中恰有一次的落点在乙上的概率;
(2)两次回球结束后,小明得分之和ξ的分布列与数学期望.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.某品牌汽车的4S店,对最近100位采用分期付款的购车者进行统计,统计结果如表所示:
(1)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位彩用分3期付款”的概率P(A);
(2)4S店销售一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款,其利润为1.5万元;分4期或5期付款,其利润为2万元.用


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
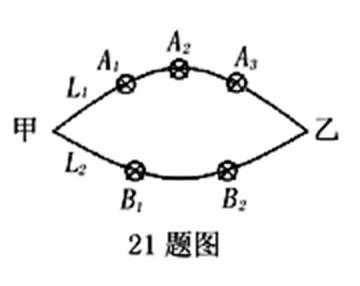
18.如图所示,张先生开车从甲地到乙地有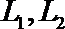
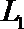
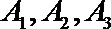

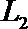
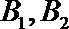
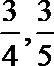
(Ⅰ)若走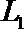
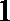
(Ⅱ)若走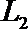
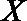
(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助张先生从上述两条路线中选择一条最好的上班路线,并说明理由.
正确答案
解:
(Ⅰ)设走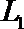
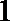
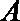
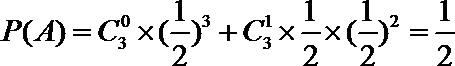
(Ⅱ)依题意,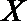
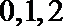
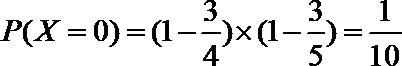
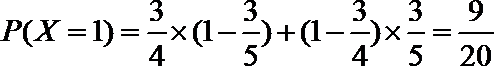
所以随机变量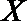
所以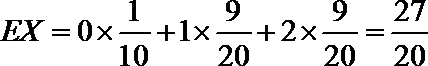
(Ⅲ)设选择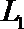
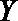
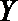
所以
因为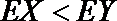

解析
解析已在路上飞奔,马上就到!
知识点
17.某班同学参加社会实践活动,对本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如右(部分有缺损):
(1)补全频率分布直方图(需写出计算过程);
(2)现从[40,55)岁年龄段样本中采用分层抽样方法抽取6人分成A、B两个小组(每组3人)参加户外体验活动,记A组中年龄在[40,45)岁的人数为


正确答案
(1)0.06;
(2)
解析
本题属于概率统计中的基本问题,题目的难度是逐渐由易到难
(1)因为第二组的频率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3所以高为0.3/5=0.06。频率直方图如下:
(2)因为[40,45)组、[45,50)组和[50,55)组的人数比为0.03:0.02:0.01=3:2:1,所以三组中应抽出的人数分别为3、2、1.




考查方向
本题考查了概率统计中的频率分布直方图和离散型随机变量的分布列和数学期望的问题.属于高考中的高频考点。
解题思路
无
易错点
1、第一问中的高为频率/组距。
2、第二问中随机变量的取值集对应的概率。
知识点
12.赌博有陷阱.某种赌博每局的规则是:赌客先在标记有








正确答案
解析
赌金的分布列为
所以
奖金的分布列为
所以
知识点
扫码查看完整答案与解析