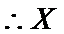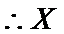- 离散型随机变量及其分布列、均值与方差
- 共180题
19.某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记

(I)求
(II)若要求

(III)以购买易损零件所需费用的期望值为决策依据,在

正确答案
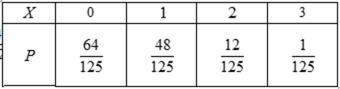
(I)x的取值为16,17,18,19,20,21,22
x的分布列:
知识点
已知2件次品和3件正品放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
17.求第一次检测出的是次品且第二次检测出的是正品的概率
18.已知每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所
需要的检测费用(单位:元),求X的分布列和均值(数学期望)
正确答案
(1)
解析
(Ⅰ)记“第一次检查出的是次品且第二次检测出的是正品”为事件

解题思路
(Ⅰ)依据题目所给的条件可以先设“第一次检查出的是次品且第二次检测出的是正品”为事件

易错点
计算事件发生的概率错误
分布列表示不出来,求相应的概率时错误,不会求数学期望。
正确答案
(2)
解析
(Ⅱ)




故

考查方向
解题思路
(Ⅱ)



易错点
分布列表示不出来,求相应的概率时错误,不会求数学期望。
18. 某卫视的大型娱乐节目现场,所有参演的节目都由甲、乙、丙三名专业老师投票决定是否通过进入下一轮,甲、乙、丙三名老师都有“通过”“待定”“淘汰”三类票各一张,每个节目投票时,甲、乙、丙三名老师必须且只能投一张票,每人投三类


(I)求某节目的投票结果获“通过”的概率;
(II)记某节目投票结果中所含“通过”和“待定”票票数之和为X,求X的分布列和数学期望.
正确答案
(1)
(2)2
解析
试题分析:本题属于离散型随机变量应用中的基本问题,题目的难度是逐渐由易到难
(Ⅰ)设“某节目的投票结果获“通过”为事件A,
则事件A包含该节目获2张“通过票”或该节目获3张“通过票”,
∵甲、乙、丙三名老师必须且只能投一张票,每人投三类票中的任意一类票的概率为
且三人投票相互没有影响,∴某节目的投票结果是最终获“通过”的概率为:
(Ⅱ)所含“通过”和“待定”票票数之和




∴

考查方向
解题思路
本题考查离散型随机变量应用,解题步骤如下:
(1)设“某节目的投票结果是最终获一等奖”为事件A,则事件A包含该节目可以获2张“获奖票”或该节目可以获3张“获奖票”,由此能求出某节目的投票结果是最终获一等奖的概率.
(2)所含“获奖”和“待定”票数之和X的值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列及数学期望.
易错点
1、第一问中弄清事件类型
2、第二问中计算不正确得不到正确结论。
知识点
某市规定,高中学生三年在校期间参加不少于






19.求抽取的200位学生中,参加社区服务时间不少于90小时的学生人数,并估计从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率;
20.从全市高中学生(人数很多)中任意选取3位学生,记



正确答案
见解析
解析
根据题意,参加社区服务时间在时间段





考查方向
解题思路
第1问根据样本数据估计总体数据,第2问先把所有可能的情况列出来,然后用频率求概率
易错点
数据收集整理出错
正确答案
见解析
解析
由19题可知,从全市高中生中任意选取1人,其参加社区服务时间不少于90小
时的概率为


所以



随机变量
因为

考查方向
解题思路
第1问根据样本数据估计总体数据,第2问先把所有可能的情况列出来,然后用频率求概率
易错点
数据收集整理出错
甲、乙两人投篮命中的概率分别为与,各自相互独立.现两人做投篮游戏,共比赛3局,每局每人各投一球.
31.求比赛结束后甲的进球数比乙的进球数多1个的概率;
32.设ξ表示比赛结束后甲、乙两人进球数的差的绝对值,求ξ的概率分布和数学期望E(ξ).
正确答案
(1)
解析
(1)比赛结束后甲的进球数比乙的进球数多1个有以下几种情况:
甲进1球,乙进0球;甲进2球,乙进1球;甲进3球,乙进2球.
所以比赛结束后甲的进球数比乙的进球数多1个的概率
P=
考查方向
解题思路
本题考查概率的求法,解题步骤如下:
(1)比赛结束后甲的进球数比乙的进球数多1个,有以下几种情况:甲进1球,乙进0球;甲进2球,乙进1球;甲进3球,乙进2球.由此能求出比赛结束后甲的进球数比乙的进球数多1个的概
率.
易错点
解题时要认真审题,注意n次独立重复试验中事件A恰好发生k次的概率计算公式的合理运用.
正确答案
(2)E(ξ)=1
解析
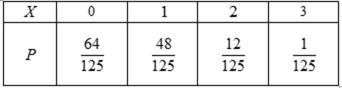
(2)ξ的取值为0,1,2,3,所以 ξ的概率分布列为
所以数学期望E(ξ)=
考查方向
解题思路
本题考查概率的求法,解题步骤如下:
(2)由已知得ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
易错点
解题时要认真审题,注意n次独立重复试验中事件A恰好发生k次的概率计算公式的合理运用.
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.
19.若直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数;
20.学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
21.在20题中调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50的学生人数为

附:
正确答案
见解析
解析
设各组的频率为


考查方向
解题思路
图和表相互结合求得,先列出可取的所有情况,然后再求期望
易错点
计算错误;读取数据时有遗漏
正确答案
见解析
解析

考查方向
解题思路
图和表相互结合求得,先列出可取的所有情况,然后再求期望
易错点
计算错误;读取数据时有遗漏
正确答案
见解析
解析
依题意9人中年级名次在1~50名和951~1000名分别有3人和6人,






考查方向
解题思路
图和表相互结合求得,先列出可取的所有情况,然后再求期望
易错点
计算错误;读取数据时有遗漏
23.为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加。现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名。从这8名运动员中随机选择4人参加比赛.
(1)设A为事件“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会”求事件A发生的概率;
(2)设X为选出的4人中种子选手的人数,求随机变量X的分布列和数学期望.
正确答案
见解析
解析
(1)由已知,有
所以事件

(2)随机变量
所以随机变量
所以随机变量
考查方向
解题思路
1利用已知条件把“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会的组合数求出,进而求出概率
易错点
本题必须注意审题,否则求解错误。
知识点
袋中共有8个球,其中有3个白球,5个黑球,这些球除颜色外完全相同.从袋中随机取出一球,如果取出白球,则把它放回袋中; 如果取出黑球,则该黑球不再放回,并且另补一个白球放入袋中.
20.重复上述过程2次后,求袋中有4个白球的概率;
21.重复上述过程3次后,记袋中白球的个数为X,求X的数学期望.
正确答案
见解析
解析
考查方向
解题思路
使用排列组合知识写出基本事件空间和4个白球个数(注意分类),并用古典概型的概率公式计算概率
易错点
本题易错在分类不清
正确答案
见解析
解析
考查方向
解题思路
分清X所有可能取值
根据情况依次求概率
写分布列以及期望
易错点
本题易错在分类不清
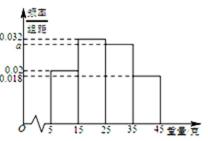
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取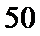
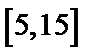
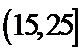
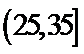
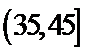
19.求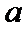
20.从盒子中随机抽取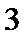
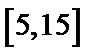

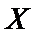
正确答案
估计盒子中小球重量的平均值约为
解析
(Ⅰ)由题意,得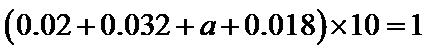
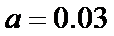
又由最高矩形中点的的横坐标为20,可估计盒子中小球重量的众数约为20(克),
而
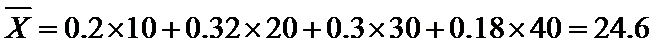
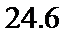
考查方向
解题思路
根据频率分布直方图求出a的值,然后根据直方图估计盒子中小球重量的众数与平均值;
易错点
不会根据频率分布直方图估计平均数;
正确答案
(2)

(或者
解析
(Ⅱ)利用样本估计总体,该盒子中小球重量在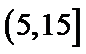
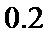
则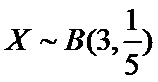

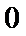
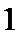
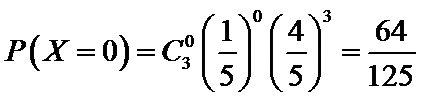
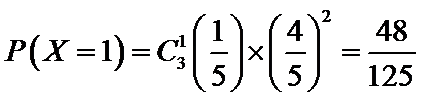
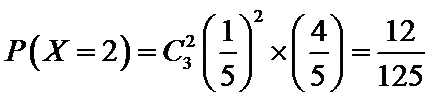
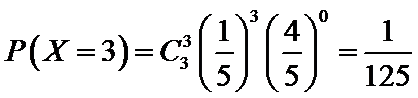

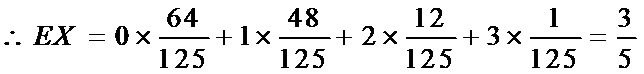
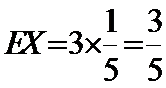
考查方向
解题思路
根据题意判断出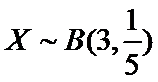
易错点
看不出二项分布导致运算很麻烦。
(4分)(2015•上海)赌博有陷阱.某种赌博每局的规则是:赌客先在标记有1,2,3,4,5的卡片中随机摸取一张,将卡片上的数字作为其赌金(单位:元);随后放回该卡片,再随机摸取两张,将这两张卡片上数字之差的绝对值的1.4倍作为其奖金(单位:元).若随机变量ξ1和ξ2分别表示赌客在一局赌博中的赌金和奖金,则 Eξ1﹣Eξ2= (元).
正确答案
0.2
知识点
扫码查看完整答案与解析