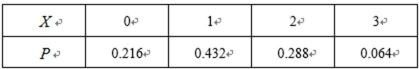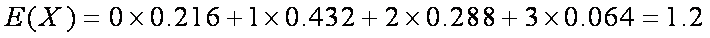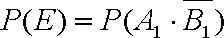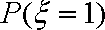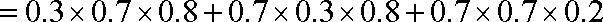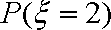- 离散型随机变量及其分布列、均值与方差
- 共180题
盒中共有9个球,其中有4个红球,3个黄球和2个绿球,这些球除颜色外完全相同。
(1)从盒中一次随机取出2个球,求取出的2个球颜色相同的概率P;
(2)从盒中一次随机取出4个球,其中红球、黄球、绿球的个数分别记为


正确答案
见解析。
解析
(1)一次取2个球共有

∴取出的2个球颜色相同的概率
(2)X的所有可能取值为
∴X的概率分布列为
故X的数学期望
知识点
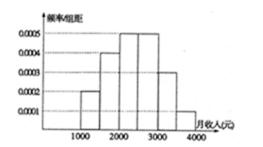
某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500) 单位:元)
(1)估计居民月收入在[1500,2000)的概率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)若将频率视为概率,从本地随机抽取3位居民(看作有放回的抽样),求月收入在[2500,3500)的居民数X的分布和数学期望。
正确答案
见解析。
解析
(1)依题意及频率分布直方图知,居民月收入在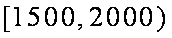
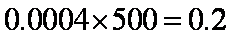
(2)频率分布直方图知,中位数在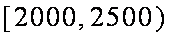
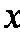
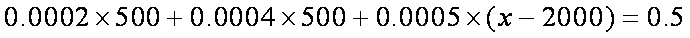
解得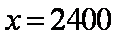
(3)居民月收入在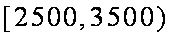
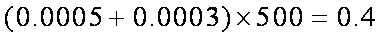
由题意知,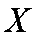
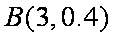
因此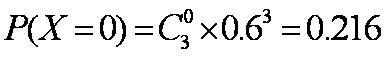
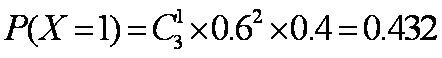
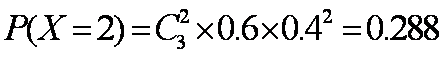
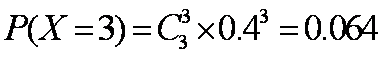
故随机变量X的分布列为
知识点
某校选拔若干名学生组建数学奥林匹克集训队,要求选拔过程分前后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔过程相互独立,根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三人合格的概率依次为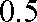



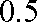
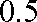
(1)求第一次选拔后甲、乙两人中只有甲合格,而乙不合格的概率;
(2)分别求出甲、乙、丙三人经过前后两次选拔后合格入选的概率;
(3)设经过前后两次选拔后合格入选的人数为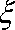
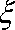
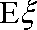
正确答案
见解析
解析
(1)分别设甲、乙经第一次选拔后合格为事件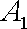
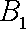
设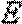
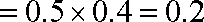
(2)分别设甲、乙、丙三人经过前后两次选拔后合格入选为事件A、B、C; 则:
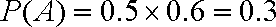
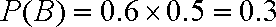
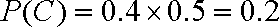
(3)经过前后两次选拔后合格入选的人数为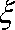
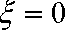
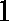
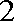

则,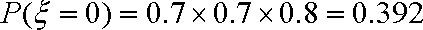
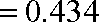
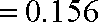
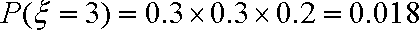
则,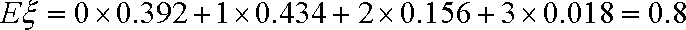
知识点
某校选拔若干名学生组建数学奥林匹克集训队,要求选拔过程分前后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔过程相互独立,根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三人合格的概率依次为





(1)求第一次选拔后甲、乙两人中只有甲合格,而乙不合格的概率;
(2)分别求出甲、乙、丙三人经过前后两次选拔后合格入选的概率;
(3)设经过前后两次选拔后合格入选的人数为


正确答案
见解析
解析
(1)分别设甲、乙经第一次选拔后合格为事件

设

(2)分别设甲、乙、丙三人经过前后两次选拔后合格入选为事件A、B、C; 则:



(3)经过前后两次选拔后合格入选的人数为




则,



则,
知识点
某次乒乓球比赛的决赛在甲乙两名选手之间举行,比赛采用五局三胜制,按以往比赛经验,甲胜乙的概率为
(1)求比赛三局甲获胜的概率;
(2)求甲获胜的概率;
(3)设甲比赛的次数为

正确答案
见解析。
解析
记甲


(1)比赛三局甲获胜的概率是:
(2)比赛四局甲获胜的概率是:
比赛五局甲获胜的概率是:
甲获胜的概率是:
(3)记乙





故甲比赛次数的分布列为:
所以甲比赛次数的数学期望是:

知识点
扫码查看完整答案与解析