- 离散型随机变量及其分布列、均值与方差
- 共180题
18. 已知

(Ⅰ)如果该同学10所高校的考试都参加,试求恰有2所通过的概率;
(Ⅱ)假设该同学参加每所高校考试所需的费用均为


正确答案
(Ⅰ)因为该同学通过各校考试的概率均为

(Ⅱ)设该同学共参加了


∵
∴所以该同学参加考试所需费用
所以
令
则
由(1)-(2)得
所以
所以

解析
解析已在路上飞奔,马上就到!
知识点
17.某次数学测验共有8道选择题,每道题共有四个选项,且其中只有一个选项是正确的,评分标准规定:每选对l道题得5分,不选或选错得0分.某考生每道题都选并能确定其中有6道题能选对,其余2道题无法确定正确选项,但这2道题中有1道题能排除两个错误选项,另1道只能排除一个错误选项,于是该生做这2道题时每道题都从不能排除的选项中随机选一个选项作答,且各题作答互不影响.
(1)求该考生本次测验选择题得40分的概率;
(2)求该考生本次测验选择题所得分数的分布列和数学期望.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.一个盒子装有六张卡片,上面分别写着如下六个函数:





(Ⅰ)从中任意拿取
(Ⅱ)现从盒子中逐一抽取卡片,且每次取出后均不放回,若取到一张写有偶函数的卡片则停止抽取,否则继续进行,求抽取次数
正确答案
(Ⅰ)





所有的基本事件包括两类:一类为两张卡片上写的函数均为奇函数;
另一类为两张卡片上写的函数为一个是奇函数,
一个为偶函数;故基本事件总数为
满足条件的基本事件为两张卡片上写的函数均为奇函数,故满足条件的基本事件个数为
故所求概率为
(Ⅱ)


故


解析
解析已在路上飞奔,马上就到!
知识点
18.移动公司进行促销活动,促销方案为顾客消费1000元,便可获得奖券一张,每张奖券中奖的概率为

(1)求
(2)试说明小李出资50元增加1张奖券是否划算。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.(某中学号召本校学生在本学期参加市创办卫生城的相关活动,学校团委对该校学生是否关心创卫活动用简单抽样方法调查了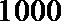
(1)完成列联表,并判断能否有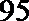
(参考数据与公式: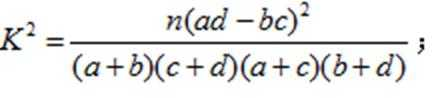
(2)已知校团委有青年志愿者100名,他们已参加活动的情况记录如下:
(i)从志愿者中任选两名学生,求他们参加活动次数恰好相等的概率;
(ii)从志愿者中任选两名学生,用
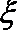

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是
(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(Ⅱ)求这名学生在上学路上因遇到红灯停留的总时间
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某种家用电器每台的销售利润与该电器的无故障时间T(单位:年)有关,若T







(Ⅰ)求
(Ⅱ)记

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 若盒中装有同一型号的灯泡共


(1) 某工人师傅有放回地连续从该盒中取灯泡

(2) 某工人师傅用该盒中的灯泡去更换会议室的一只已坏灯泡,每次从中取一灯泡,若是正品则用它更换已坏灯泡,若是次品则将其报废(不再放回原盒中),求成功更换会议室的已坏灯泡所用灯泡只数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某工厂2011年第一季度生产的A,B,C,D四种型号的产品产量用条形图表示如图,现用分层抽样的方法从中选取50件样品,参加四月份的一个展销会.

(1)问A,B,C,D型号的产品各抽取多少件?从50件样品中随机的抽取2件,求这两件产品恰好是不同型号的产品的概率;
(2)从A,C型号的产品中随机的抽取3件,用ξ表示抽取A种型号的产品件数,求ξ的分布列和数学期望.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析