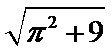- 旋转体(圆柱、圆锥、圆台)
- 共25题
12.已知圆锥的侧面展开图是一个半径为3,圆心角为
正确答案
解析
∵圆锥侧面展开图是一个圆心角为120°半径为3的扇形∴圆锥的母线长为
形的弧长为

考查方向
解题思路
由于圆锥侧面展开图是一个圆心角为

易错点
本题必须注意圆锥侧面展开图是一个圆心角120°半径为3的扇形
知识点
12.一矩形的一边在


正确答案
解析
设矩形与函数

矩形绕





考查方向
解题思路
1.先根据题意确定

易错点
对于函数

知识点
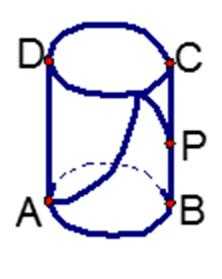
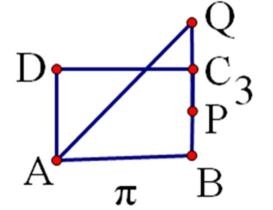
11. 如图,有一圆柱开口容器(下表面封闭),其轴截面是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒的所经过的最短路程是( )
正确答案
解析
如图,展开后作辅助线,使得QC=CP,则AQ即为所求最小距离,利用勾股定理可得D选项是正确的。
考查方向
解题思路
将图像展开之后,通过等价转化,最后变成两点间的距离来求解。
易错点
不知道怎样将圆柱展开。。
知识点
8.圆锥的侧面展开图是圆心角为π,面积为2π的扇形,则圆锥的体积是___________
正确答案
解析
2πr=πl, 2π=πrl.得:r=,l=2,h=1.V=π
考查方向
解题思路
本题考查运用圆锥侧面积求底面半径及母线,再求高,进而求体积。解题步骤如下:2πr=πl, 2π=πrl.得:r=,l=2,h=1.V=π
易错点
本题必须注意审题,忽视则会出现错误。
知识点
13.将边长为2的等边三角形以其一边为轴旋转一周,则形成的几何体的表面积是 。
正确答案
4√3π
解析
试题分析:本题属于复数的运算问题,题目的难度较小。注意共轭复数即可。
考查方向
本题主要考查了旋转体的表面积。
解题思路
本题考查旋转体的表面积,解题步骤如下:
旋转体为2个等大的圆锥,高为1,母线长为2,底面半径为√3,所以S=4√3π。
易错点
本题必须注意扇形面积公式,忽视则会出现错误。
知识点
扫码查看完整答案与解析