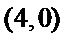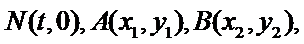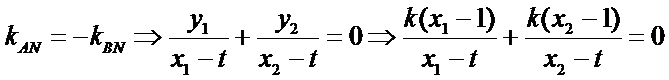- 直线与圆的位置关系
- 共80题
1.设P是圆(x-3)2+(y+1)2=4上的动点,Q是直线x=-3上的动点,则|PQ|的最小值为( )
正确答案
解析
由题意知,圆的圆心坐标为(3,-1),圆的半径r=2,|PQ|的最小值为圆心到直线x=-3的距离减去圆的半径长,所以|PQ|min=3-(-3)-2=4.
知识点
4.在平面直角坐标系中,A和B分别是x轴和y轴上的动点,若以AB为直径的圆C与直线2x+y-4=0相切,则圆C周长的最小值为( )
正确答案
解析
设直线2x+y-4=0与圆C相切于点D
∵∠AOB=90°,∴点O在圆C上,则点C与点O间的距离等于点C到直线2x+y-4=0的距离
∴点C在以O为焦点,以直线2x+y-4=0为准线的抛物线上
∴当且仅当O,C,D共线时,圆的直径最小为|OD|.
又|OD|=
∴圆C的半径最小为
∴圆C周长的最小值为2π×

知识点
10.若直线y=x+b与曲线y=3-
正确答案
解析
曲线方程可化简为(x-2)2+(y-3)2=4(1≤y≤3)
即表示圆心为(2,3)半径为2的半圆,
依据数形结合,当直线y=x+b与此半圆相切时,须满足圆心(2,3)到直线y=x+b的距离等于2,
∴

因为是下半圆,如图
所以b=1-
解得b=3,所以1-
知识点
15.直线l: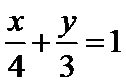
正确答案
(x-1)2 +(y-1)2=1
解析
设△OAB的内切圆的方程为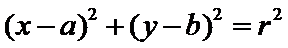
由题意得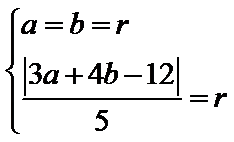
解得
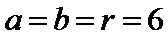
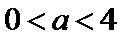
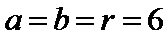
故所求圆的方程为(x-1)2 +(y-1)2=1 。
考查方向
解题思路
1.先利用待定系数法设出圆的方程;
2.根据圆与三角形的各边均相切列出方程组,求出内切圆的方程。
易错点
1.无法根据题意射出圆的方程,感觉无从下手;
2.处理数据出错导致答案不正确。
知识点
20.已知直线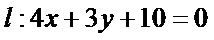
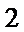
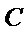
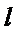
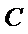
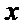
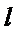
(Ⅰ)求圆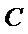
(Ⅱ)过点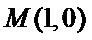
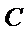
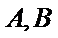
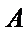
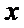
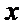
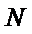
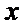
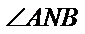
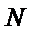
正确答案
(Ⅰ)
(Ⅱ)存在N
解析
试题分析:本题是直线与圆的位置关系的常见题型,运算量较大。此类问题往往要用到韦达定理,设而不求等方法技巧,把几何关系转化为代数运算。
(Ⅰ)设圆心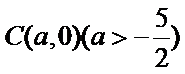
则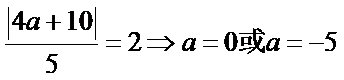
所以圆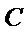
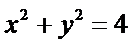
(Ⅱ)当直线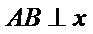
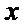
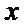
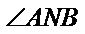
当直线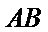
设直线
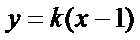
联立圆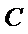
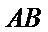
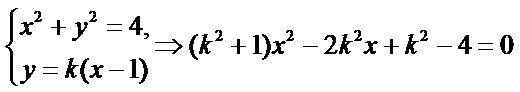
故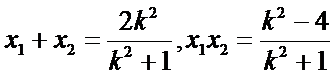
若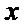
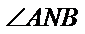
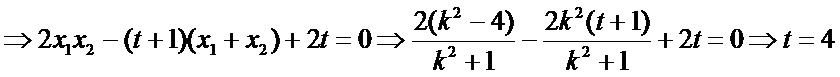
当点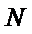
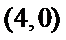
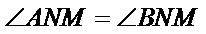
考查方向
解题思路
本题主要考查圆的标准方程、直线与圆的位置关系、点到直线的距离公式等基础知识,
解题步骤如下:根据直线与圆相切的定义,求出圆方程;由直线与圆的位置关系,建立方程组,结合韦达定理,和斜率关系,得出结果。
易错点
第一问易忽视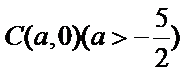
第二问不能理解“若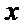
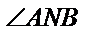
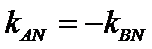
知识点
扫码查看完整答案与解析