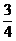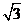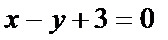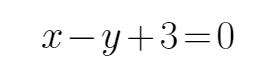- 直线与圆的位置关系
- 共80题
15.已知直线l：
正确答案
4
知识点
圆x2+y2−2x−8y+13=0的圆心到直线ax+y−1=0的距离为1，则a=( )
A−
B−
C
D2
正确答案
知识点
13.若直线
正确答案
2
解析
由
考查方向
解题思路
先求出圆心到直线的距离后利用点到直线的距离公式即可。
易错点
不知道题中给出的120度如何转换导致出错。
知识点
14.已知M,N是圆
正确答案
解析
∵圆
圆
∴MN的方程为
∴
∴
考查方向
解题思路
先求出两圆的公共弦MN的方程，然后利用点B到直线MN的距离求出高BE，利用勾股定理求出MN即可
易错点
本题必须注意利用两圆相间得到公共弦方程
知识点
3.在区间
A
B
C
D
正确答案
解析
因为直线
考查方向
解题思路
1)用圆心到直线的距离小于半径，得到
2)用
易错点
本题易将几何概型当成古典概型去做，只取整数点比较.
知识点
13．已知直线过圆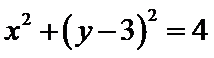
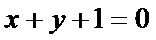
正确答案
解析
由题意可知，直线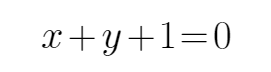
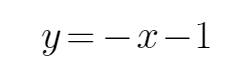
考查方向
直线与圆的关系，直线的方程
解题思路
根据直线和直线垂直，然后求直线斜率，进而求直线的方程
易错点
相关公式掌握不牢固
知识点
10．已知圆C：
A
B
C
D
正确答案
解析
如图，
设与直线
考查方向
解题思路
先要找到圆上哪一部分点到直线
易错点
本题容易因为不理解几何概型的角度模型而导致错误的产生。
知识点
7．已知圆心为（2，0）的圆C与直线y=x相切，求切点到原点的距离 ( )
A1
B
C2
D
正确答案
解析
先画图由相切得圆心到直线的距离就是半径长，再用勾股定理计算出切点到原点的距离为
考查方向
解题思路
由相切求出半径长，再用勾股定理计算
易错点
相切关系的刻画
知识点
7．已知条件
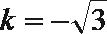
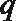
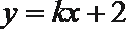
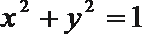
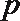
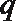
正确答案
解析
直线和圆相切由d=r得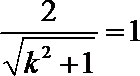
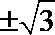
考查方向
本题主要考查充要条件的概念及直线 和圆的位置关系。
解题思路
直线和圆相切得出k值，再进行判断。
易错点
充要条件的概念不清。
知识点
8．从圆
A
B
C
D0
正确答案
解析
圆x2-2x+y2-2y+1=0的圆心为M（1，1），半径为1，从外一点P（3，2）向这个圆作两条切线，则点P到圆心M的距离等于
考查方向
本题主要考查了圆的切线方程；
解题思路
先求出点P到圆心M的距离等于
易错点
本题易在圆外一点求圆的切线方程，注意数形结合；
知识点
扫码查看完整答案与解析