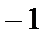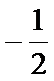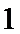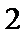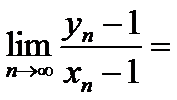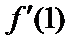- 数列的极限
- 共21题
1
题型:填空题
|
14.无穷数列{an}由k个不同的数组成,Sn为{an}的前n项和.若对任意的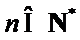
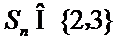
正确答案
解析
由于 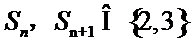
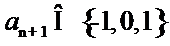
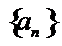
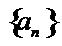
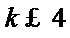
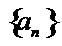
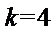
考查方向
推理
解题思路
归纳,推理
易错点
推理的切入点
知识点
数列与函数的综合数列的极限
1
题型:简答题
|
23.已知数列




(1)能否唯一确定数列

(2)能否求得
(3)若





正确答案
(1)
即
由于

因此不能唯一确定数列
(2)为使
为使

∴ 


(3)

∴ 

∴
解析
解析已在路上飞奔,马上就到!
知识点
由an与Sn的关系求通项an数列的极限数列与不等式的综合
1
题型:填空题
|
12.若

正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
数列的极限
1
题型:简答题
|
23.若数列




已知数列



(1)求证:数列
(2)若

(3)当

正确答案
(1)因为
所以
所以数列
(2)
所以
当
设
则
当
设
则
因为
所以
即:
解得:
(3)当
则
当
当
即:
解析
解析已在路上飞奔,马上就到!
知识点
等比数列的判断与证明数列的极限数列与不等式的综合
1
题型:
单选题
|
18.设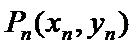
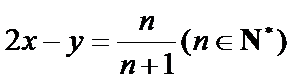
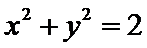
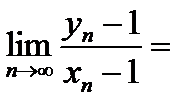
正确答案
A
解析
当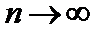
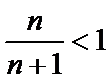
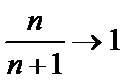
而由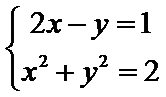
所以
而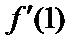
又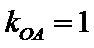
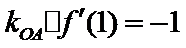
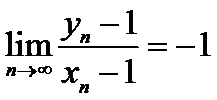
故选A.
知识点
数列的极限数列与解析几何的综合直线与圆相交的性质
下一知识点 : 数列与不等式的综合
扫码查看完整答案与解析