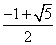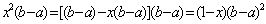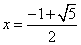- 数列与不等式的综合
- 共81题
已知等差数列{an}满足:a1=2,且a1,a2,a5成等比数列。
(1)求数列{an}的通项公式;
(2)记Sn为数列{an}的前n项和,是否存在正整数n,使得Sn>60n+800?若存在,求n的最小值;若不存在,说明理由。
正确答案
见解析。
解析
(1)设数列{an}的公差为d,依题意,2,2+d,2+4d成比数列,故有(2+d)2=2(2+4d),
化简得d2﹣4d=0,解得d=0或4,
当d=0时,an=2,
当d=4时,an=2+(n﹣1)•4=4n﹣2。
(2)当an=2时,Sn=2n,显然2n<60n+800,
此时不存在正整数n,使得Sn>60n+800成立,
当an=4n﹣2时,Sn=
令2n2>60n+800,即n2﹣30n﹣400>0,
解得n>40,或n<﹣10(舍去),
此时存在正整数n,使得Sn>60n+800成立,n的最小值为41,
综上,当an=2时,不存在满足题意的正整数n,
当an=4n﹣2时,存在满足题意的正整数n,最小值为41
知识点
商家通常依据“乐观系数准则”确定商品销售价格,及根据商品的最低销售限价a,最高销售限价b(b>a)以及常数x(0<x<1)确定实际销售价格c=a+x(b-a),这里,x被称为乐观系数。
经验表明,最佳乐观系数x恰好使得(c-a)是(b-c)和(b-a)的等比中项,据此可得,最佳乐观系数x的值等于_____________。
正确答案
解析
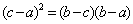
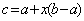
又b>a可得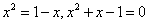
知识点
已知等差数列



(1)若

(2)若

正确答案
(1)

(2)
解析
本小题主要考查等比等差数列、等比数列和不等式等基础知识,考查运算求解能力,考查函数与方程思想、化归与转化思想。
(1)因为数列


所以
即


(2)因为数列


所以
即
知识点
对于








(1)b2+b4+b6+b8=__;
(2)记cm为数列{bn}中第m个为0的项与第m+1个为0的项之间的项数,则cm的最大值是___.
正确答案
(1)3;(2)2.
解析
(1)观察知

一次类推





b2+b4+b6+b8=3;(2)由(1)知cm的最大值为2.
知识点
在数列









(1)试写出数列
(2)如果





(3)如果



正确答案
见解析
解析
(1)解:答案不唯一. 如3项子列:


(2)证明:由题意,知

因为 




(3)证明:由题意,设


因为




设 


当


所以 
当




所以
因为 


综上, 
知识点
扫码查看完整答案与解析