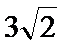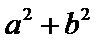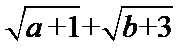- 不等式
- 共9题
14.设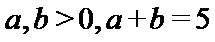
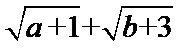
正确答案
解析
由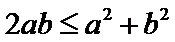
得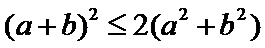
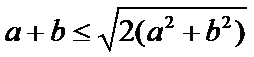
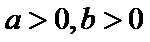
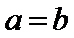
从而有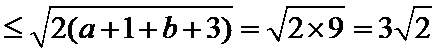
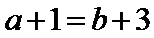
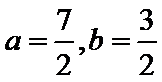
故填: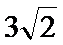
考查方向
解题思路
】本题考查应用基本不等式求最值,先将基本不等式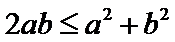
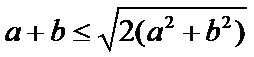
易错点
本题属于中档题,注意等号成立的条件.
知识点
请考生在(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题记分. 请考生将所选题目后面的小矩形框涂黑。
22.选修4-1:几何证明选讲
如图,已知PA是



(1)求
(2)求AE的长.
23.选修4-4:坐标系与参数方程
已知圆


(1)把圆

(2)求经过两圆交点的直线的极坐标方程。
24.选修4-5:不等式选讲
已知不等式
(1)求实数m的取值范围;
(2)在(1)的条件下,当实数m取得最大值时,试判断
正确答案
22.
23.
24.
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第 22、 23、 24三题中任选一题做答。注意:只能做选定的题目。如果多做,则按所做的第一题计分。
22.选修 4-1:几何证明选讲
如图所示,已知








Ⅰ.求证:
Ⅱ.若


23. 选修 4-4:坐标系与参数方程
在极坐标系下,已知圆
Ⅰ.求圆

Ⅱ.当


24. 选修 4-5:不等式选讲
设函数
Ⅰ.解不等式
Ⅱ.已知关于


正确答案
22.答案:(I)证明:∵DE2=EF•EC,∠DEF公用,
∴△DEF∽△CED,∴∠EDF=∠C.又∵弦CD∥AP,∴∠P=∠C,
∴∠EDF=∠P,∠DEF=∠PEA ∴△EDF∽△EPA.
∴
∴CE•EB=EF•EP .
(II)∵DE2=EF•EC,DE=3,EF=2. ∴32=2EC,∴
∵CE:BE=3:2,∴BE=3.
由(I)可知:CE•EB=EF•EP,∴

∴BP=EP﹣EB=
∴

23.(Ⅰ)圆O:ρ=cosθ+sinθ,即ρ2=ρcosθ+ρsinθ,
所以圆O的直角坐标方程为:x2+y2=x+y,即x2+y2﹣x﹣y=0.
直线



也就是ρsinθ﹣ρcosθ=1.
则直线l的直角坐标方程为:y﹣x=1,即x﹣y+1=0.
(Ⅱ)由

故直线l与圆O公共点为(0,1),该点的一个极坐标为
24.(Ⅰ)∵f(x)=|2x+1|﹣|x﹣3|=
∴①当x<﹣
②当﹣

③当x>3时,x+4>0,∴x>3.
综上所述,不等式f(x)>0的解集为:(﹣∞,﹣4)∪(

∴当x≤﹣



当x≥3时,x+4≥7,综上所述,f(x)≥﹣
∵关于x的不等式a+3<f(x)恒成立,∴a<f(x)﹣3恒成立,
令g(x)=f(x)﹣3,则g(x)≥﹣
∴g(x)min=﹣
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分,作答时标出所选题目的题号。
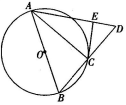
22.几何证明选讲 如图,AB是圆O的直径,点C在圆O上,延长BC到D,使BC=CD,过点C作圆O的切线交AD于E。
(Ⅰ)求证:CE⊥AD;
(Ⅱ)若AB=2,ED=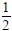
23.坐标系与参数方程在直角坐标系xOy中,圆C的参数方程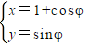
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)直线l的极坐标方程是ρ(sinθ+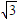
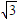
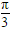
24. 不等式选讲 已知函数f (x)=|x-1|.
(Ⅰ)解不等式f (x)+f (x+4)≥8;
(Ⅱ)若|a|<1,|b|<1,且a≠0,求证: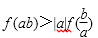
正确答案
22.
23.
24.
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析