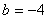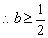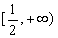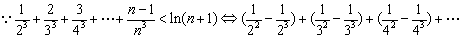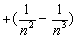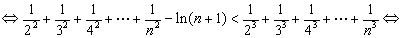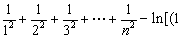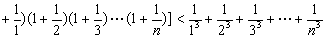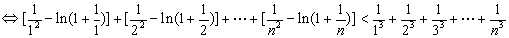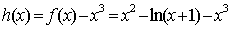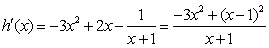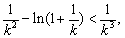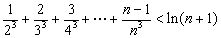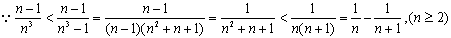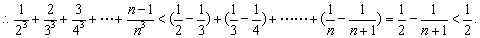- 二次函数与幂函数
- 共2034题
若


正确答案
解析
略
知识点
已知函数





(1)求
(2)若


正确答案
见解析
解析
(1)由题意,



(2)


若




故

若




故

综上,当且仅当

当且仅当

当

知识点
对


(1)求证:

(2)若直线






(3)对















正确答案
见解析
解析
(1)由





并且对

(2)由题设及(1)的结论,两个函数图像有且仅有一个公共点,即方程

整理方程得
由

此时方程的两个实数根


得
因为



(3)当


且
① 当







对于函数




此时方程



(16分)
② 当





综上,当





知识点
设m,k为整数,方程
正确答案
解析
设
















知识点
已知向量序列:



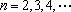
若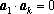
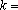
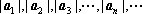
正确答案
9,3
解析
略
知识点
设函数



正确答案

解析
本题主要考查函数恒成立问题的基本解法,属于难题。
依据题意得



当





知识点
设函数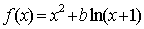
(1)若对于定义域内的任意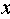
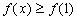
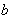
(2)若函数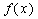
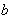
(3)求证: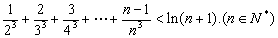
正确答案
见解析。
解析
(1)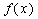
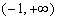
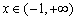
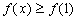
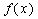


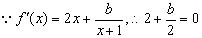
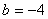
经检验,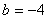
(2)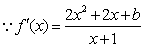
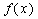
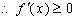
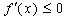
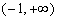
若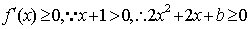
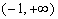
即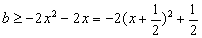
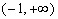
若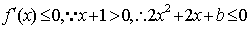
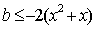

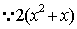
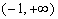
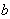
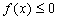
综上所知,实数
(2)法一
令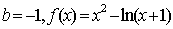
当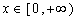
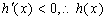
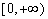
又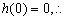
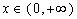

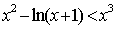
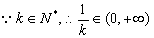
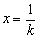
则有

法二:
又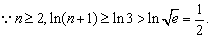
知识点
若1﹣i(i是虚数单位)是关于x的方程x2+2px+q=0(p、q∈R)的一个解,则p+q=( )
正确答案
解析
∵1﹣i(i是虚数单位)是关于x的方程x2+2px+q=0(p、q∈R)的一个解,
∴1+i是此方程的另一个解。
根据根与系数的关系可得

∴p+q=﹣1+2=1。
故选C。
知识点
在



(1)求角
(2)求

正确答案
见解析
解析
(1)由已知
由余弦定理


∵

(2)∵



∵




此时
知识点
直线

正确答案
解析
联立方程求得交点分别为
所以阴影部分的面积为
知识点
扫码查看完整答案与解析