- 二次函数与幂函数
- 共2034题
设函数
(1)求函数
(2)当



正确答案
见解析。
解析
(1)
则

且当

即

扣分)。
(2)当

当


所以


知识点
如图,平面PAD


(1)求证:PB
(2)在线段CD上是否存在一点Q,使得点A到平面EFQ的距离为0.8,若存在,求出CQ的长,若不存在,请说明理由。
正确答案
见解析。
解析
解析:(1)证:设


(2)由题意易得















又

知识点
有下列命题:
①若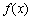
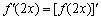
②若函数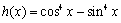
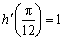
③若函数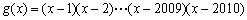
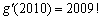
④若三次函数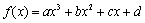
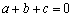
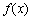
其中真命题的序号是() 。
正确答案
③
解析
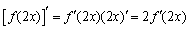
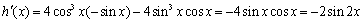
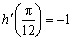
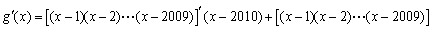
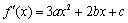
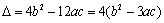
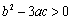
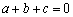
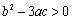
知识点
设函数
(1)当

(2)证明:对

(3)若


正确答案
见解析
解析
(1)


则
令

当



当



所以 


(2)因为 
所以 
所以当




(3)(证法一)数学归纳法
ⅰ)当
ⅱ)假设当
即若

当





设
由(2)得
=
=
由假设可得 
所以当 
由ⅰ),ⅱ)可知,对一切正整数n∈N*,命题都成立,
所以 若


(证法二)若
那么由(2)可得

……………………13分
知识点
已知

正确答案
1
解析
略
知识点
一厂家向用户提供的一箱产品共10件,其中有1件次品,用户先对产品进行随机抽检以决定是否接收,抽检规则如下:至多抽检3次,每次抽检一件产品(抽检后不放回),只要检验到次品就停止继续抽检,并拒收这箱产品;若3次都没有检验到次品,则接收这箱产品,按上述规则,该用户抽检次数的数学期望是 。
正确答案
2.7
解析
略
知识点
已知


正确答案
解析
略
知识点
高二某班共有60名学生,其中女生有20名,三好学生占
正确答案
解析
略
知识点
函数

正确答案
解析
略
知识点
已知函数

(1)若


(2)求函数
正确答案
见解析
解析
解:(1)当
当





即
(2)


1)当





故


2)当





故


知识点
扫码查看完整答案与解析





































