- 两角和与差的余弦函数
- 共32题
1
题型:
单选题
|
4.已知sinα·sinβ=1,那么cos(α+β)的值是( )
正确答案
A
解析
由sinα·sinβ=1,得

因此cos(α+β)=cosαcosβ-sinαsinβ=-1.
知识点
三角函数的化简求值两角和与差的余弦函数
1
题型:简答题
|
19.已知向量




(1)求角
(2)若


正确答案
(1)








(2)由

及




解析
解析已在路上飞奔,马上就到!
知识点
两角和与差的余弦函数二倍角的余弦余弦定理平面向量数量积的运算
1
题型:简答题
|
15.△ABC的三个内角为A、B、C,若

正确答案
1
解析
由题可知,A=45o,可求得tanA=1.本题主要考查了三角函数的公式化简。
考查方向
本题主要考查了三角函数的公式化简。
解题思路
解题步骤如下:利用两角和差公式求解。
易错点
本题要注意公式的化简。
知识点
三角函数中的恒等变换应用两角和与差的余弦函数两角和与差的正弦函数
1
题型:填空题
|
14.已知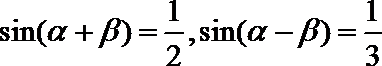

正确答案
1
解析
由题可知,将展开的两式相加减,可求出tana/tanb=5,代入对数式得值为1.
考查方向
本题主要考查了两角和差公式及对数运算
解题思路
本题考查两角和差公式及对数运算,解题思路如下:利用两角和差公式展开已知,两式相加减,求出正切值;代入对数式求解。
易错点
本题必须注意两角和差公式
知识点
对数的运算性质弦切互化两角和与差的余弦函数两角和与差的正弦函数
1
题型:简答题
|
19.(1)求证:sinα·sinβ=
(2)在锐角△ABC中,∠ A=60°,BC=2,求△ABC面积的取值范围.
正确答案
(1)略;(2)
解析
试题分析:本题属于三角函数中的基本问题,题目的难度是逐渐由易到难.
(1)由

两式相减得:
(2)由正弦定理可知,
由
所以
考查方向
本题考查了三角函数的积化和差的证明及解三角形的问题.属于高考中的高频考点。
解题思路
本题考查三角函数问题,解题步骤如下:
(1)利用两角和差公式证明。
(2)利用正余弦定理求解。
易错点
注意锐角三角形的条件,忽视则容易出错。
知识点
两角和与差的余弦函数正弦定理
下一知识点 : 两角和与差的正弦函数
扫码查看完整答案与解析






