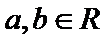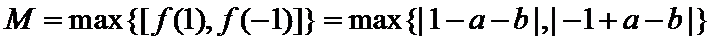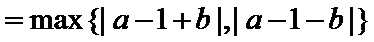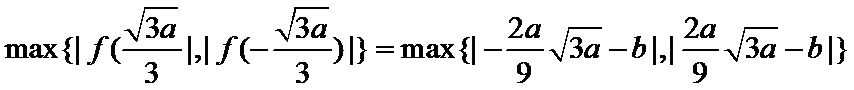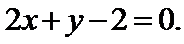- 复合函数的单调性
- 共281题
4.下列函数中,在区间
正确答案
知识点
设函数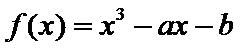
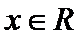
26.求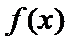
27.若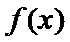
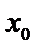
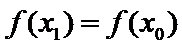
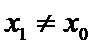
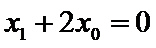
28.设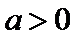
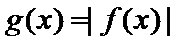
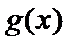
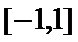
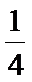
正确答案
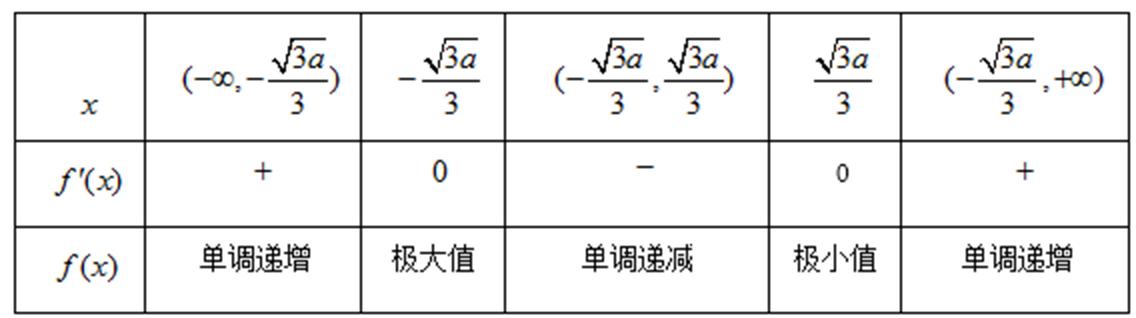
(Ⅰ)递减区间为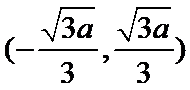
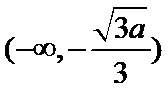
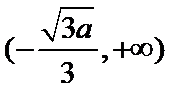
解析
本题主要考察了导数的运算,利用导数研究函数的性质、证明不等式等知识点,属于拔高题,不容易得分,解析如下:
试题解析:(1)解:由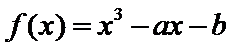
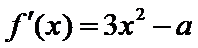
①当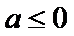
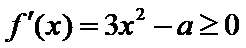
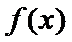
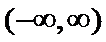
②当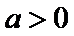
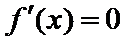
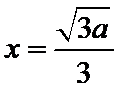
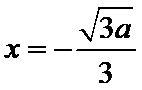
当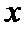
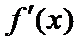
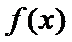
所以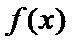
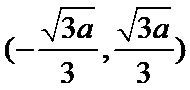
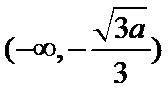
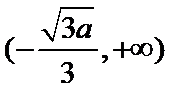
考查方向
解题思路
(Ⅰ)先求函数的导数: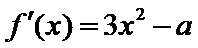
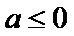
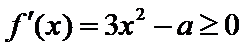
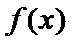
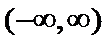
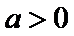
易错点
第二问不知如何就参数的范围进行讨论导致失分。
正确答案
(Ⅱ)证明:因为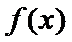
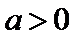
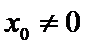
由题意得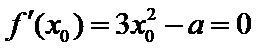
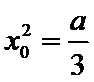
进而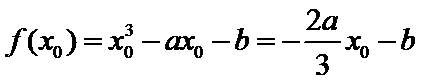
又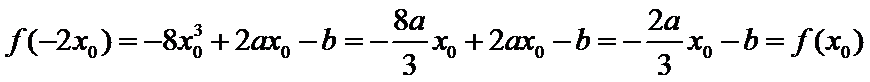
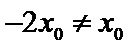
由题意及(1)知,存在唯一实数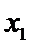
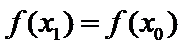
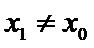
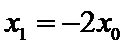
所以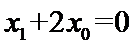
解析
本题主要考察了导数的运算,利用导数研究函数的性质、证明不等式等知识点,属于拔高题,不容易得分.
考查方向
解题思路
(Ⅱ)由题意得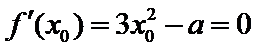
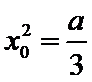
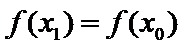
易错点
第二问不知如何就参数的范围进行讨论导致失分。
正确答案
(3)证明:设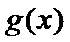
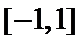
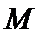
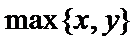
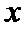
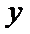
①当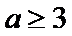
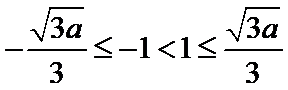
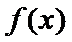
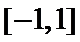
所以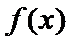
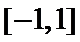
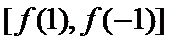
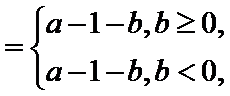
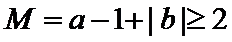
②当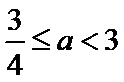
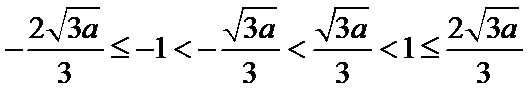
由(1)和(2) 知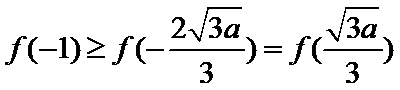
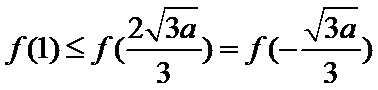
所以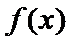
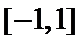
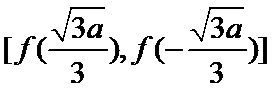
所以
③当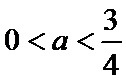
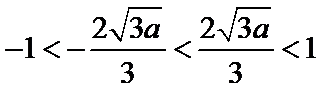
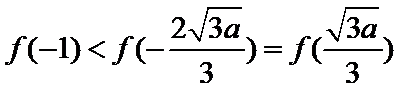
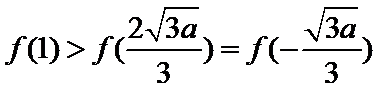
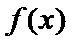
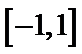
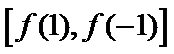
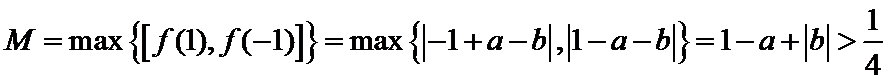
综上所述,当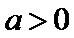
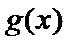
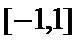
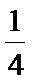
解析
本题主要考察了导数的运算,利用导数研究函数的性质、证明不等式等知识点,属于拔高题,不容易得分.
考查方向
解题思路
(Ⅲ)实质研究函数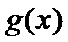
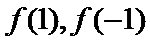
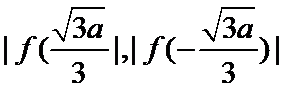
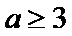
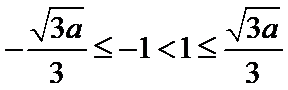
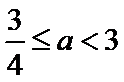
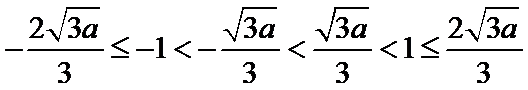
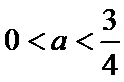
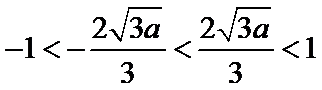
易错点
第二问不知如何就参数的范围进行讨论导致失分。
11.函数
正确答案
解析
因为


考查方向
解题思路
化三角函数为同角同名三角函数,正确运用诱导公式二倍角公式化简,变为二次函数求最值。
易错点
求解本题易出现的错误是忽略


知识点
20. 已知函数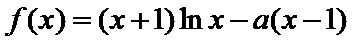
(I)当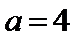
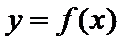
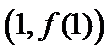
(II)若当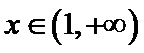
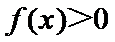
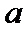
正确答案
(Ⅰ)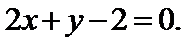
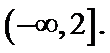
解析
(I)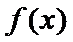
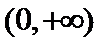
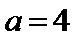
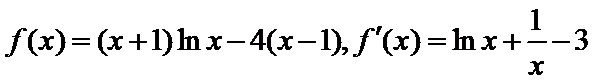
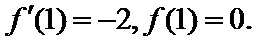
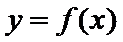
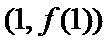
(II)当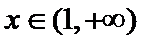
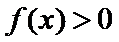
令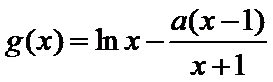
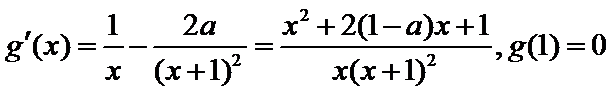
(i)当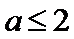
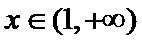
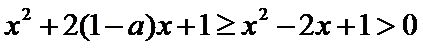
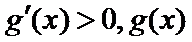
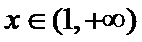
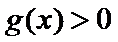
(ii)当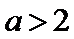
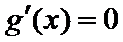
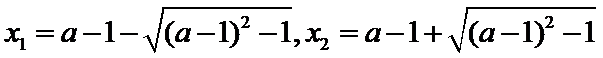
由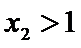
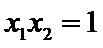
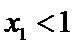
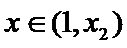
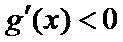
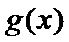
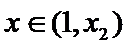
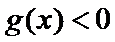
综上,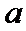
考查方向
解题思路
(Ⅰ)先求函数的定义
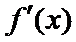
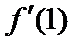
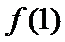
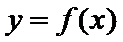
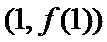
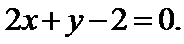
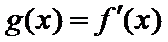
易错点
用导数构造新函数并用导数继续研究新函数,分类讨论。
知识点
4.下列函数中,既是偶函数又存在零点的是( )
正确答案
解析
选项A:

选项B:

选项C:
选项D:
且

考查方向
解题思路
根据偶函数和零点的性质,结合选项,逐一判断。
易错点
对函数的零点的概念掌握不好,不会判断函数有无零点
知识点
17.已知点 






正确答案
解析
设直线








即


所以



考查方向
解题思路
设直线






易错点
旋转前后的坐标问题
知识点
8.若



正确答案
解析
因为







考查方向
解题思路
先求导,然后利用函数极值,结合基本不等式求解。
易错点
函数求导错误,想不到是运用基本不等式求解
知识点
14. 若函数



正确答案
解析
因为函数f(x)是偶函数
所以








作出函数f(x)的图象如图:
要使函数g(x)=f(x)-b有4个零点,
则-6<b<0,
故答案为:(-6,0)
考查方向
函数的综合性质的应用,根的存在性及根的个数的判断
解题思路
根据函数f(x)是偶函数,结合函数与x轴交点个数得到f(0)=0,根据函数与方程之间的关系转化为两个函数的交点问题进行求解即可.
易错点
作图错误,分类讨论错误
知识点
6. 函数


正确答案
解析
由题可知:A=1,T=π,则w=2,φ=-π/12.所以

A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
利用三角函数的图像性质,即可得到结果。
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在表示待定系数时发生错误。
知识点
10.已知偶函数



正确答案
解析



考查方向
本题考试抽象函数的单调性和函数奇偶性的认识.
解题思路
根据偶函数的特点,函数图像关于y轴对称,在y轴的两侧函数的单调性互异性及f(x)=f(-x)转化,求出
易错点
对抽象函数的认识有限,对函数的单调性和奇偶性认识不够深刻。
教师点评
通过本题可考察学生对函数奇偶性和单调性综合题的理解,同时考查了分类讨论的思想。
知识点
扫码查看完整答案与解析