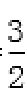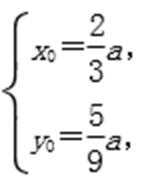直线的一般式方程
共31题

· 直线的一般式方程

直线的一般式方程
共31题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 16 分

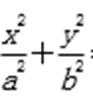
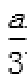
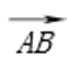
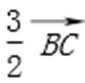
在平面直角坐标系xOy中，点C在椭圆M：＝1(a＞b＞0)上．若点A(－a，0)，B(0，)，且＝．

20.求椭圆M的离心率；

21.设椭圆M的焦距为4，P，Q是椭圆M上不同的两点，线段PQ的垂直平分线为直线l，且直线l不与y轴重合．

①若点P(－3，0)，直线l过点(0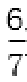，－)，求直线l的方程；

②若直线l过点(0，－1) ，且与x轴的交点为D，求D点横坐标的取值范围．

第(1)小题正确答案及相关解析

正确答案

（1）；

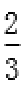
解析

解：（1）设C (x0，y0)，则＝(a，)，＝(x0，y0－)．

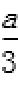
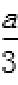
因为＝，所以(a，)＝ (x0，y0－)＝，

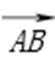
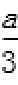
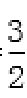
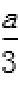
得

代入椭圆方程得a2＝．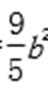

因为a2－b2＝c2，所以e＝．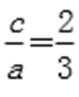

考查方向

本题考查椭圆的离心率的求法，注意运用斜率的共线的坐标表示和点满足椭圆方程，考查直线方程和椭圆方程联立，运用韦达定理和中点坐标公式，考查化简整理的运算能力本题考查了利用三角函数的函数单调区间和解三角形求面积

解题思路

本题考查直线与椭圆位置关系，解题步骤如下：

（1）设C（m，n），由向量共线的坐标表示，可得C的坐标，代入椭圆方程，可得a，b的关系，

再由离心率公式计算即可得到所求值；

（2）①由题意可得c=2，a=3， b2＝5，可得椭圆方程，设直线PQ的方程为y=k（x+3），代入椭圆方程，运用韦达定理和中点坐标公式，再由两直线垂直的条件：斜率之积为-1，解方程可得k，进而得到所求直线方程；

②设直线PQ的方程为y=kx+m，代入椭圆方程可得，运用韦达定理和中点坐标公式，再由两直线垂直的条件，求得4m=5+9k2，再由中点在椭圆内，可得k的范围，再由直线l的方程可得D的横坐标的范围．

易错点

第二问容易计算错误

第(2)小题正确答案及相关解析

正确答案

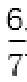
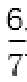
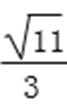
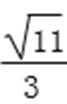
（2）①y＝－x＋或y＝－x＋②(－，0)∪(0，)

解析

解：（2）①因为c＝2，所以a2＝9，b2＝5，所以椭圆的方程为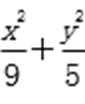＝1，

设Q (x0，y0)，则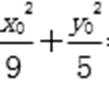＝1．……①

因为点P(－3，0)，所以PQ中点为，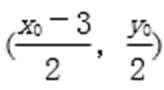

因为直线l过点(0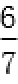，－)，直线l不与y轴重合，所以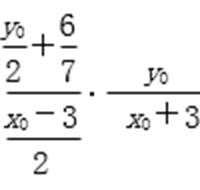x0≠3，

所以＝－1，

化简得x02＝9－y02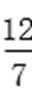－y0．……②

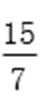
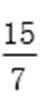
将②代入①化简得y02－y0＝0，解得y0＝0（舍），或y0＝．

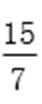
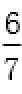
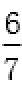
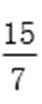
将y0＝代入①得x0＝±，所以Q为(±，)，

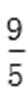
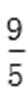
所以PQ斜率为1或，直线l的斜率为－1或－，

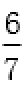
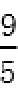
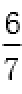
所以直线l的方程为y＝－x＋或y＝－x＋．

②设PQ：y＝kx+m，则直线l的方程为：y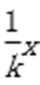＝－－1，所以xD＝－k．

将直线PQ的方程代入椭圆的方程，消去y得(5＋9k2)x2＋18kmx＋9m2－45＝0．…………①，

设P(x1，y1)，Q(x2，y2)，中点为N，

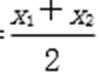
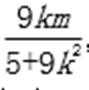
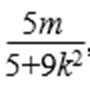
xN＝＝－，代入直线PQ的方程得yN＝，

代入直线l的方程得9k2＝4m－5． ……②

又因为△＝(18km)2－4(5＋9k2) (9m2－45)＞0，

化得m2－9k2－5＜0．

将②代入上式得m2－4m＜0，解得0＜m＜4，

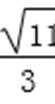
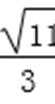
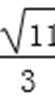
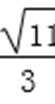
所以－＜k＜，且k≠0，所以xD＝－k∈(－，0)∪(0，)．

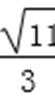
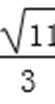
综上所述，点D横坐标的取值范围为(－，0)∪(0，)．

考查方向

解题思路

本题考查直线与椭圆位置关系，解题步骤如下：

（1）设C（m，n），由向量共线的坐标表示，可得C的坐标，代入椭圆方程，可得a，b的关系，

再由离心率公式计算即可得到所求值；

易错点

第二问容易计算错误

题型：简答题

简答题 · 16 分

18.如图，在平面直角坐标系xOy中，已知椭圆的离心率为，且右焦点F到左准线l的距离为3.

（1）求椭圆的标准方程；

（2）过F的直线与椭圆交于A，B两点，线段AB的垂直平分线分别交直线l和AB于点P，C，若PC=2AB，求直线AB的方程.

正确答案

（1）由题意，得且，

解得，，则，

所以椭圆的标准方程为．

（2）当轴时，，又，不合题意．

当与轴不垂直时，设直线的方程为，，，

将的方程代入椭圆方程，得，

则，的坐标为，且

．

若，则线段的垂直平分线为轴，与左准线平行，不合题意．

从而，故直线的方程为，

则点的坐标为，从而．

因为，所以，解得．

此时直线方程为或．

解析

解析已在路上飞奔，马上就到！

知识点

直线的一般式方程椭圆的定义及标准方程直线与椭圆的位置关系

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 直线的一般式方程与直线的垂直关系

百度题库 > 高考 > 理科数学 > 直线的一般式方程

扫码查看完整答案与解析