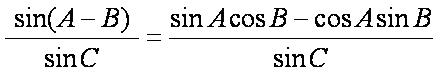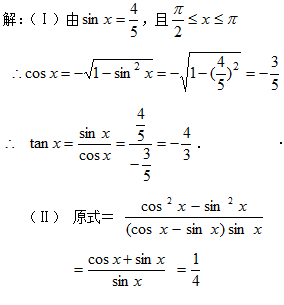- 三角恒等变换
- 共635题
定义:设W是由一平面内的n(n≥3)个向量组成的集合。若a
中除a外的所有向量和的模,则称a是W的极大向量,下列命题:
①若W中每个向最量方向都相同,则W中必存在一个极大向最;
②给定平面内两个不共线向里a、b,在该平面内总存在唯一的平面向里c,使得
W={a,b,c}中的每个元索都是极大向jg ;
③若

一个元素也都是极大向量,其中真命题的个数是
正确答案
解析
略
知识点
在△ABC中,已知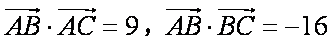
(1)AB的值;
(2)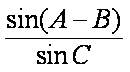
正确答案
见解析。
解析
(1)(方法1)因为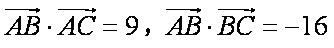
所以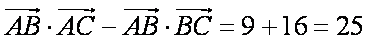
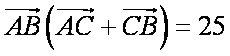
亦即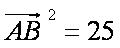

(方法2)设A,B,C的对边依次为a,b,c,
则由条件得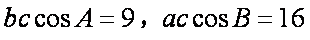
两式相加得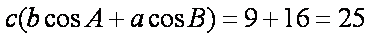
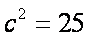
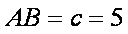
(方法3)设A,B,C的对边依次为a,b,c,
则由条件得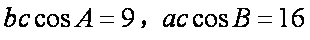
由余弦定理得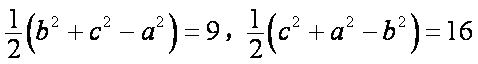
两式相加得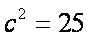
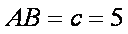
(2)
由正弦定理得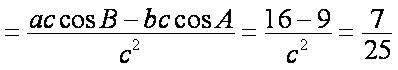
知识点
若tanα=3,则
正确答案
解析


∵tanα=3,
∴

∴
知识点
已知










正确答案
解析
,由正弦定理




知识点
(1)已知

(2)化简
正确答案
见解析。
解析
(1)

(2)



知识点
已知


(1)求角
(2)若
正确答案
见解析。
解析
(1)∵




∵


(2)由题知
∴

∴

而


知识点
12.实数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知A,B,C是△ABC的三内角,向量
(1)求角A;
(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知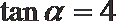
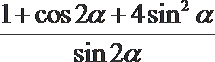
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知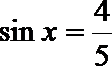
(Ⅰ)求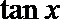
(Ⅱ)求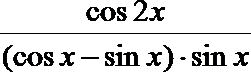
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析