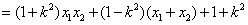- 诱导公式的推导
- 共79题
设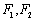
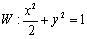
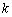
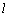
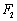
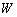
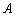
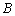
(1)求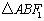
(2)如果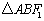
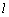
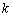
正确答案
(1)
(2)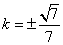
解析
(1)解:椭圆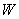
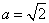
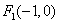
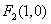
由椭圆的定义,得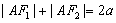
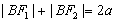
所以
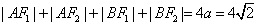
(2)解:因为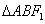
所以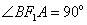
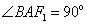
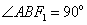
当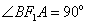
设直线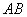
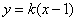
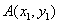
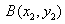
由 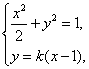
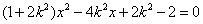
所以 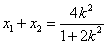
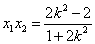
由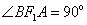
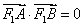
因为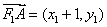
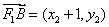
所以
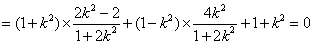
解得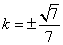
当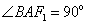
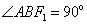
则点A在以线段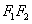
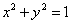
由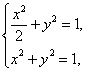
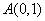
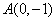
根据两点间斜率公式,得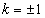
综上,直线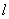
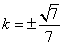
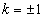
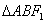
知识点
执行右面的程序框图,若输入的


正确答案
3
解析
根据判断条件

输入
第一次判断后循环,
第二次判断后循环,
第三次判断后循环,
第四次判断不满足条件,退出循环,输出
知识点
已知斜率为1的直线1与双曲线C:
(1)求C的离心率;
(2)设C的右顶点为A,右焦点为F,|DF|·|BF|=17证明:过A、B、D三点的圆与x轴相切。
正确答案
见解析。
解析
(1)
由题设知,

代入C的方程,并化简,得
设

则
由

故

故

(2)由①、②知,C的方程为:

故不妨设



又



故
连接MA,则由




所以过A、B、D三点的圆与
知识点
将外形和质地一样的4个红球和6个白球放入同一个袋中,将它们充分混合后,现从中取出4个球,取出一个红球记2分,取出一个白球记1分,若取出4个球总分不少于5分,则有________种不同的取法。
正确答案
195
解析
略
知识点
已知定义域是

(1)对任意
(2)当
①对任意
②函数

③存在
④“函数

“
其中正确结论的序号是__________.
正确答案
解析
略
知识点
扫码查看完整答案与解析