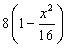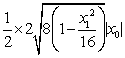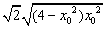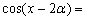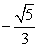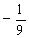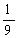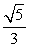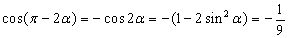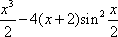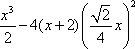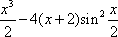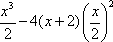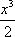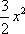- 弧度与角度的互化
- 共39题
若函数
正确答案
解析
略
知识点
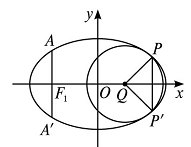
如图,椭圆的中心为原点
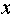
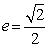
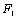
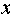
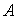
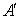
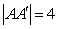
(1)求该椭圆的标准方程;
(2)取平行于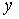
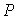
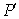
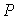
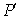
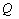

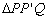
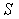
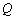
正确答案
见解析
解析
(1)由题意知点A(-c,2)在椭圆上,则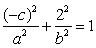
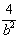
由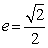
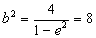
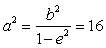
故该椭圆的标准方程为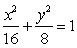
(2)由椭圆的对称性,可设Q(x0,0)。
又设M(x,y)是椭圆上任意一点,则
|QM|2=(x-x0)2+y2
=x2-2x0x+x02+
=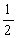
设P(x1,y1),由题意,P是椭圆上到Q的距离最小的点,因此,上式当x=x1时取最小值,
又因x1∈(-4,4),所以上式当x=2x0时取最小值,从而x1=2x0,且|QP|2=8-x02.
由对称性知P′(x1,-y1),故|PP′|2=|2y1|,
所以S=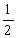
=
=
=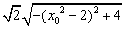
当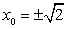
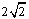
此时对应的圆Q的圆心坐标为Q(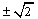
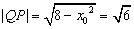
因此,这样的圆有两个,其标准方程分别为(x+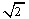
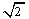
知识点
已知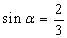
正确答案
解析
本题考查了二倍角公式及诱导公式,∵ sina=2/3,
∴
知识点
A. 如图,圆




圆





求证:
正确答案
见解析
解析
证明:连结AO1,并延长分别交两圆于点E和点D连结BD、CE,因为圆O1与圆O2内切于点A,所以点O2在AD上,故AD,AE分别为圆O1,圆O2的直径。
从而
于是
所以AB:AC为定值
设
解得
由题设知,椭圆的长半轴长


故所求直线的斜率为
原不等式可化为
解得
所以原不等式的解集是
知识点
(1)证明:当x∈[0,1]时,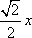
(2)若不等式ax+x2+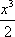
正确答案
见解析
解析
(1)证明:记F(x)=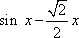
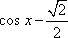
当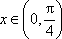

当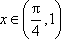

又F(0)=0,F(1)>0,所以当x∈[0,1]时,F(x)≥0,即sin x≥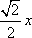
记H(x)=sin x-x,则当x∈(0,1)时,H′(x)=cos x-1<0,所以,H(x)在[0,1]上是减函数,则H(x)≤H(0)=0,即
sin x≤x.
综上,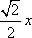
(2)解法一:因为当x∈[0,1]时,
ax+x2+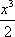
=(a+2)x+x2+
≤(a+2)x+x2+
=(a+2)x.
所以,当a≤-2时,
不等式ax+x2+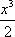
下面证明,当a>-2时,
不等式ax+x2+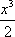
因为当x∈[0,1]时,
ax+x2+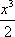
=(a+2)x+x2+
≥(a+2)x+x2+
=(a+2)x-x2-
≥(a+2)x-
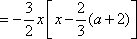
所以存在x0∈(0,1)(例如x0取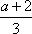

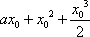
即当a>-2时,
不等式ax+x2+
综上,实数a的取值范围是(-∞,-2]。
解法二:记f(x)=ax+x2+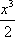
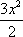
记G(x)=f′(x),则
G′(x)=2+3x-4sin x-2(x+2)cos x.
当x∈(0,1)时,cos x>
G′(x)<2+3x-4·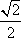
=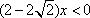
于是f′(x)在[0,1]上是减函数,因此,当x∈(0,1)时,f′(x)<f′(0)=a+2,故当a≤-2时,f′(x)<0,从而f(x)在[0,1]上是减函数,所以f(x)≤f(0)=0,即当a≤-2时,不等式ax+x2+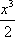
下面证明,当a>-2时,
不等式ax+x2+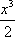
由于f′(x)在[0,1]上是减函数,且f′(0)=a+2>0,f′(1)=a+
当a≥6sin 1-2cos 1-
当-2<a<6sin 1-2cos 1-
所以,当a>-2时,
不等式ax+x2+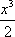
综上,实数a的取值范围是(-∞,-2]。
知识点
扫码查看完整答案与解析