- 频率分布表
- 共48题
19.某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5。现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
(1)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a,b,c的值;
(2)在(1)的条件下,将等级系数为4的3件日用品记为x1,x2,x3,等级系数为5的2件日用品记为y1,y2,现从x1,x2,x3,y1,y2这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率。
正确答案
(1)由频率分布表得a+0.2+0.45+b+c=1, a+b+c=0.35
因为抽取的20件日用品中,等级系数为4的恰有3件,所以b=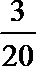
等级系数为5的恰有2件,所以c=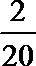
从而a=0.35-b-c=0.1
所以a=0.1 b=0.15 c=0.1
(2)从日用品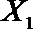
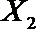
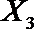
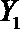
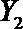
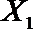
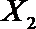
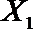

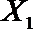
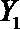
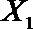
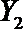
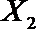
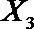
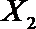
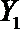
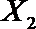
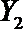
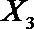
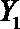
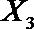
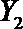
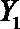
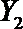
设事件A表示
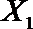
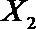
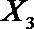
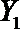
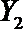
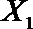
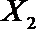
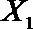
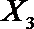
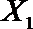
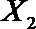
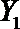
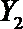
故所求的概率P(A)= 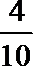
解析
解析已在路上飞奔,马上就到!
知识点
16. 某品牌汽车
已知分3期付款的频率为0.2,该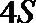
(Ⅰ)求上表中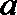
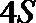
(Ⅱ)该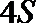
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,且等可能向左向右滚下,最后掉入编号为
规定小球掉入
(1)分别求
(2)假设中奖的概率为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.国家教育部、体育总局和共青团中央曾共同号召,在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动.为此某网站于2010年1月18日至24日,在全国范围内进行了持续一周的在线调查,随机抽取其中200名大中小学生的调查情况,就每天的睡眠时间分组整理如下表所示:
(Ⅰ)估计每天睡眠时间小于8小时的学生所占的百分比约是多少;
(Ⅱ)该网站利用上边的算法流程图,对样本数据作进一步统计
正确答案
解:(Ⅰ)由样本数据可知,每天睡眠时间小于8小时的频率是

由此估计每天睡眠时间小于8小时的学生约占88%.
(Ⅱ)输入

流程图进入一个求和状态.
设




故输出的S值为6.7.
S的统计意义是指被调查者每天的平均睡眠时间估计为6.7小时.
解析
解析已在路上飞奔,马上就到!
知识点
3.为了解今年某校高三毕业班准备报考飞行员学生的体重(单位:kg)情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为
正确答案
48
解析
解析已在路上飞奔,马上就到!
知识点
17.某校为了解学生的视力情况,随机抽查了一部分学生视力,将调查结果分组,分组区间为(3.9,4.2],(4.2,4.5],…,(5.1,5.4].经过数据处理,得到如下频率分布表:
(Ⅰ)求频率分布表中未知量n,x,y,z的值;
(Ⅱ)从样本中视力在(3.9,4.2]和(5.1,5.4]的所有同学中随机抽取两人,求两人的视力差的绝对值低于0.5的概率.
正确答案
(1)n=50,x=50,y14,z=0.28;(2)
解析
试题分析:本题属于用样本估计总体与古典概型综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
(I)由表可知,样本容量为n,
由(5.1,5.4]一组频数为2,频率为0.04,则
由
y=50﹣3﹣6﹣25﹣2=14,
(II)设样本视力在(3.9,4.2]的3人为a,b,c;样本视力在(5.1,5.4]的2人为d,e.
由题意从5人中任取两人的基本事件空间为:Ω={(a,d),(a,e),(b,d),(b,e),(c,d),(c,e),(a,b),(a,c),(b,c),(d,e)},共10个基本事件;
设事件A表示“抽取的两人的视力差的绝对值低于0.5”,则事件A包含的基本事件有:(a,b),(a,c),(b,c),(d,e),共4个基本事件;
P(A)=

故抽取的两人的视力差的绝对值低于0.5的概率为
考查方向
解题思路
(1)由表中数据求解;
(2)根据古典概型求解.
易错点
相关知识点不熟容易处错。
知识点
18.某校对高一年级学生寒假参加社区服务的次数进行了统计,随机抽取了M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:
(Ⅰ)求表中n, p的值和频率分布直方图中
(Ⅱ)如果用分层抽样的方法从样本服务次数在[10,15)和[25,30)的人中共抽取6人,再从这6人中选2人,求2人服务次数都在[10,15)的概率.
正确答案
见解析
解析
(Ⅰ)
因20÷



中位数位于区间
则0.125x=0.25,所以x=2,所以学生参加社区服务次数的中位数为17次。
(Ⅱ)
由题意知样本服务次数在[10,15)有20人,样本服务次数在[25,30)有4人. 如果用分层抽样的方法从样本服务次数在[10,15)和[25,30)的人中共抽取6人,则抽取的服务次数在[10,15)和[25,30)的人数分别为:

记服务次数在[10,15)为

从已抽取的6人中任选两人的所有可能为:
共15种.设“2人服务次数都在[10,15)”为事件

共10种,
所以
考查方向
解题思路
根据表和图的信息,仔细求解
易错点
作图,遗漏数据
知识点
19. 某城市






分组的频率分布直方图如图:
(Ⅰ)求直方图中
(Ⅱ)求月平均用电量的众数和中位数;
(Ⅲ)在月平均用电量为





正确答案
(1)
(2)众数为230,中位数为224;
(3)5户
解析
试题分析:本题第(1)、(2)问属于统计中的基础知识,难度不大;第(3)问是统计中的常见问题,只要掌握了分层抽样的知识,也很容易解决,需要在计算的时候细心。
(Ⅰ)依题意:
解得
(Ⅱ)由直方图可知,月平均用电量的众数为230.
设中位数为

解得
(Ⅲ)月平均用电量为






考查方向
解题思路
1、根据频率分布直方图中所有小矩形的面积之和等于1求出x,同时利用相关知识求出众数和中位数;
2、先求出分布区间内的居民总户数,然后利用分层抽样的方法进行解决。
易错点
本题容易因对频率分布直方图的认识不到位而导致计算出错;
知识点
12.某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末位数记为x,那么x的值为________
正确答案
2
解析
由题可知,(180+181+171+172+174+175+170+x)/5=175,解得:x=2
考查方向
解题思路
本题考查统计的知识,解题思路如下:利用平均数的计算求出x即可
易错点
本题必须注意茎叶图的读数规则
知识点
据统计,2015年“双11”天猫总成交金额突破






女性消费情况:
男性消费情况:
19.计算


20.若消费金额不低于



附:
(

正确答案
解析
试题分析:本题属于概率和独立性检验的问题,(1)考查古典概型和分层抽样,(2)独立性检验的思想。解:依题意,女性应抽取

抽出的










设“选出的两名网购者恰好是一男一女”为事件
事件


考查方向
解题思路
(1)根据分层抽样求出男女各抽的人数,然后用穷举法列举出基本事件的总数,找到要求的基本事件的个数,用古典概型公式可以算出其概率,
(2)利用独立性检验的方法解出。
易错点
不知道应用古典概型公式来计算。
正确答案
有关.
解析
试题分析:本题属于概率和独立性检验的问题,(1)考查古典概型和分层抽样,(2)独立性检验的思想。

则
答:我们有99%的把握认为“是否为‘网购达人’”与性别有关
考查方向
解题思路
(1)根据分层抽样求出男女各抽的人数,然后用穷举法列举出基本事件的总数,找到要求的基本事件的个数,用古典概型公式可以算出其概率,
(2)利用独立性检验的方法解出。
易错点
不知道应用古典概型公式来计算。
扫码查看完整答案与解析