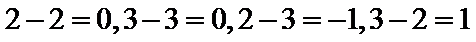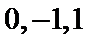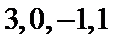- 等差数列的前n项和及其最值
- 共119题
已知




22.设

23.设 
正确答案
(Ⅰ)⑴

∴
解析
本题属于数列知识的综合应用问题,属于中档题,只要掌握相关的知识,即可解决本题,解析如下:⑴

∴
考查方向
解题思路
(Ⅰ)先根据等比中项定义得:

易错点
对裂项相消法求和的方法不熟悉导致出错。
正确答案
(Ⅱ)⑵
由已知
将
∴
解析
本题属于数列知识的综合应用问题,属于中档题,只要掌握相关的知识,即可解决本题,解析如下:⑵
由已知
将
∴
考查方向
解题思路
(


易错点
对裂项相消法求和的方法不熟悉导致出错。
3.已知等差数列

正确答案
知识点
11.无穷数列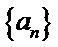
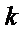
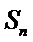
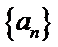
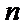
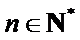
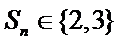
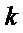
正确答案
解析
根据题意,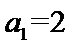
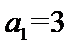
∵
∴从第二项开始,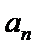
由题意无穷数列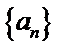
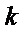
那么在同一个数列中,它们只可能是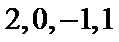
∴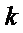
考查方向
易错点
没有厘清关系,无从着手.
知识点
10.从区间












正确答案
解析
试题分析:利用几何概型,圆形的面积和正方形的面积比为

考查方向
解题思路
先确定几何度量,再根据几何概型的概率计算公式即可求解。
易错点
不能准确选择几何度量导致出错。
知识点
15.已知各项均为正数的数列




正确答案
解析
考查方向
解题思路
把已知数列递推式变形,
易错点
本题是从第二项起为等比数列,所以和要分段求得。
知识点
6.设公差不为0的等差数列

正确答案
19
解析
设首项为

∴
考查方向
解题思路
利用基本量法解不等式组,解出首项和公差,表示a10即可
易错点
运用基本量解题,计算容易出现错误
知识点
16.设Sn是数列{an}的前n项和,且a1=-1,an+1=Sn Sn+1,则Sn=________.
正确答案
知识点
7.已知等差数列





正确答案
解析
根据题意可知,
由
所以
考查方向
等差数列的前N项和,等差数列的最大项
解题思路
根据题意,前五项和和前九项和相等,所以可以得到前7项和最大
易错点
等差数列性质掌握不好
知识点
7.已知等差数列





正确答案
知识点
扫码查看完整答案与解析