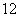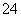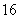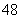- 排序问题与算法的多样性
- 共9题
已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥n,l

正确答案
解析
因为m⊥α,l⊥m,l
又因为m,n为异面直线,所以α与β相交,且l平行于它们的交线,故选D
知识点
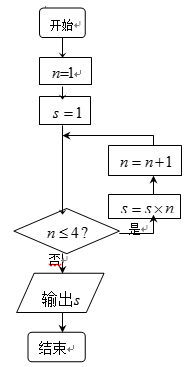
程序框图的运算结果为 ( )
正确答案
解析
当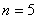
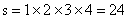
知识点
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5,
(1)求证:AA1⊥平面ABC;
(2)求二面角A1-BC1-B1的余弦值;
(3)证明:在线段BC1上存在点D,使得AD⊥A1B,并求
正确答案
见解析
解析
(1)因为AA1C1C为正方形,所以AA1⊥AC.
因为平面ABC⊥平面AA1C1C,且AA1垂直于这两个平面的交线AC,所以AA1⊥平面ABC.
(2)由(1)知AA1⊥AC,AA1⊥AB.
由题知AB=3,BC=5,AC=4,所以AB⊥AC.
如图,以A为原点建立空间直角坐标系A-xyz,则B(0,3,0),A1(0,0,4),B1(0,3,4),C1(4,0,4)。
设平面A1BC1的法向量为n=(x,y,z),
则
令z=3,则x=0,y=4,所以n=(0,4,3)。
同理可得,平面B1BC1的法向量为m=(3,4,0)。
所以cos〈n,m〉=
由题知二面角A1-BC1-B1为锐角,
所以二面角A1-BC1-B1的余弦值为
(3)设D(x,y,z)是直线BC1上一点,且

所以(x,y-3,z)=λ(4,-3,4)。
解得x=4λ,y=3-3λ,z=4λ.
所以
由


因为
此时,
知识点
如果执行右面的框图,输入N =5,则输出的数等于( )
正确答案
解析
(1)



(3)

(4)

(5)

知识点
在航天员进行的一项太空实验中,要先后实施

正确答案
96
解析
略
知识点
扫码查看完整答案与解析