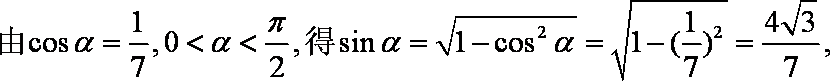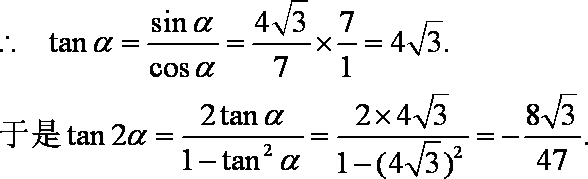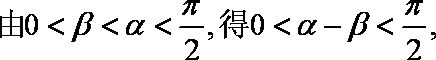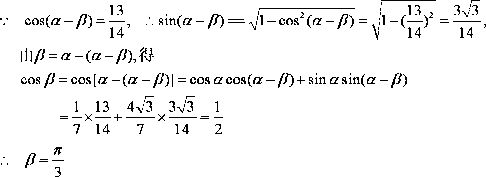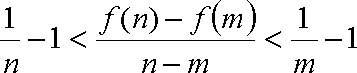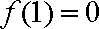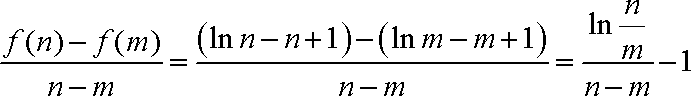- 求函数y=Asin(ωx+φ)的解析式
- 共127题
已知



(1)求证:数列

(2)设数列



正确答案
见解析。
解析
(1)

所以




(2) 

对于任意的





知识点
某人要测量一座山的高度,他在山底所在的水平面上,选取在同一直线上的


正确答案
解析
设山顶为D,在底部的射影为E,设DE=h,则AE=

知识点
已知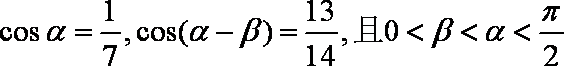
(1)求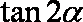
(2)求β。
正确答案
见解析。
解析
(1)
(2)
知识点
已知

(1)求角C;
(2)求
正确答案
见解析
解析
(1)
又
(2)
知识点
如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的体积是( )
正确答案
解析
由三视图可知:该几何体是两个同底的半圆锥,其中底的半径为1,高为

因此体积=2×

故选D
知识点
已知数列



(1)若

(2)设




正确答案
见解析。
解析
(1)若




两边取对数,得
化为
因为
所以数列


所以

(2)由

当

①

由已知


因为


所以

因为

所以

知识点
已知函数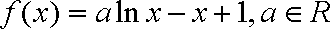
(1)求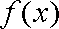
(2)若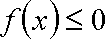
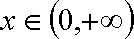
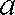
(3)对任意的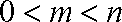
正确答案
见解析
解析
(1)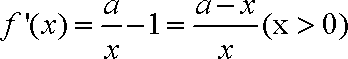
当
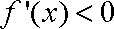
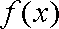
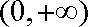
当
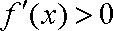
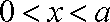
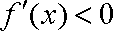

∴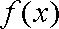
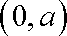
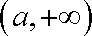
(2)由(1)知:当
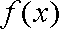
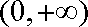
∴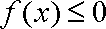
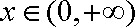
当
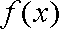
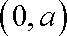
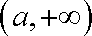
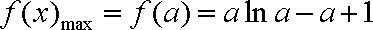
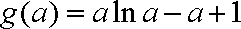
依题意有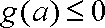
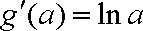
∴
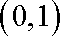
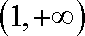
∴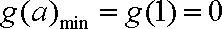
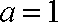
(3)由(2)知: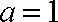
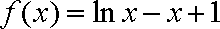
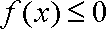
即
则
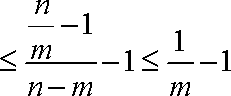
又由
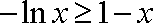
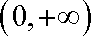
∴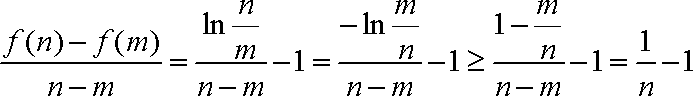
综上所述:对任意的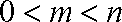
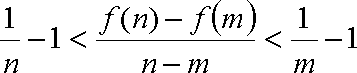
知识点
如图,已知矩形








(1)求证:
(2)若点




正确答案
见解析
解析
(1)连接




由勾股定理得
折起后,平面





得

又


(2)在



(1)中已证明













知识点
已知曲线





(1)求曲线
(2)若点






正确答案
见解析
解析
(1)


将




(2)设
所以
代入




知识点
设函数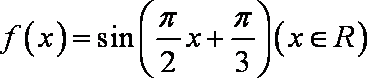
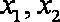
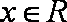
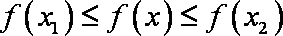
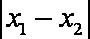
正确答案
2
解析
略
知识点
扫码查看完整答案与解析