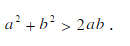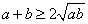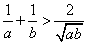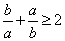- 排列数公式的推导
- 共36题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
圆


(1)求
(2)椭圆





正确答案
(1)双曲线C1的方程为
(2)直线l的方程为:

解析
(1)设切点P(x0,y0),(x0>0,y0>0),则切线的斜率为
可得切线的方程为
令x=0,可得

∴切线与x轴正半轴,y轴正半轴围成一个三角形的面积S=

∵4=

∴

由题意可得

故双曲线C1的方程为
(2)由(1)可知双曲线C1的焦点(±
可设椭圆C2的方程为
把P


因此椭圆C2的方程为
由题意可设直线l的方程为x=my+
联立

∴

∴x1+x2=

x1x2=



∵

∴

∴


因此直线l的方程为:

知识点
选修4-5:不等式选讲
设函数



(1)求M;
(2)当

正确答案
见解析
解析
(1)由f(x)=2|x﹣1|+x﹣1≤1 可得

解①求得1≤x≤
综上,原不等式的解集为[0,
(2)由g(x)=16x2﹣8x+1≤4,求得﹣




∵当x∈M∩N时,f(x)=1﹣x,x2f(x)+x[f(x)]2 =xf(x)[x+f(x)]
=


故要证的不等式成立。
知识点
如图,在






正确答案
解析
解法1。取





所以
于是
在

即

解法2。设


在

所以
在


所以
知识点
若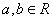
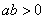
正确答案
解析
∵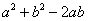
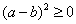
对B、C,当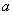
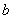
对D,∵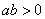
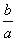
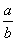
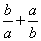
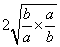
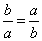
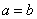
知识点
扫码查看完整答案与解析