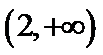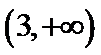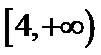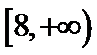- 平面向量的综合题
- 共11题
15.



①




正确答案
①④⑤
解析
∵等边三角形ABC的边长为2,



∵



∴
考查方向
解题思路
根据题意逐一判断序号。
易错点
平面向量的基本性质混淆,向量的数量积求解错误,计算能力弱
知识点
15.平面向量






小值是 .
正确答案
解析
试题分析:依题意可知




考查方向
解题思路
对
易错点
相关知识点不熟悉导致出错。
知识点
17.已知


(1)求
(2)在




与


正确答案
解析
试题分析:本题属于向量结合三角函数以及解三角形的问题,题目的难度是逐渐由易到难,(1)直接根据题意得到函数的解析式再使用辅助角公式合二为一化简之后再求单调区间;(2)利用正余弦定理来解三角形。
(1)由题意知





(2)






因为向量


由正弦定理得

考查方向
解题思路
本题考查向量结合三角函数以及解三角形的问题,解题步骤如下:(1)直接根据题意得到函数的解析式再使用辅助角公式合二为一化简之后再求单调区间;(2)利用正余弦定理来解三角形。
易错点
第一问忘记写
知识点
10.已知点P是函数y=sin(2x+θ)图像与x轴的一个
交点,A,B为P点右侧同一周期上的最大值和最小
值点,则

正确答案
解析
可以考虑特殊情况,即当θ=0时来做,故p可以选择原点,AB两点的坐标也很容易表示出来,所以利用向量的数量积的坐标运算可得


考查方向
解题思路
可以找一种特殊情况来做。
易错点
不会求其数量积。
知识点
15.已知












①
②
③
④
则在区间

正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
设向量



正确答案
解析
由题意可得

故点Q的坐标为(
由点Q在y=f(x)的图象上运动可得
消掉x1可得y=2sin2x,即y=f(x)=2sin2x
故可知最大值及最小正周期分别是2,π,
故选C
知识点
10.在平面直角坐标系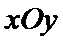
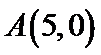
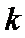
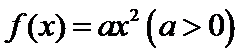
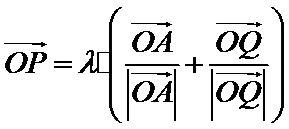
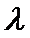
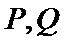
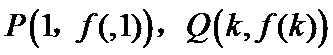
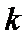
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在平面直角坐标系








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知向量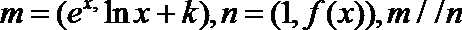
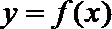
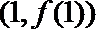
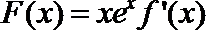
(1)求k的值及F(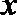
(2)已知函数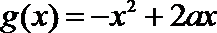
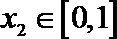
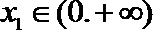
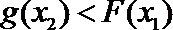
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知平面向量a=(

(1)证明a⊥b;
(2)若存在不同时为零的实数k和t,使x=a+ (t2–3)b,y=–ka+tb,且x⊥y,试求函数关系式k=f(t);
(3)据(2)的结论,讨论关于t的方程f(t)–k=0的解的情况。
正确答案
(1)证明:∵a·b=
(2)解:∵x⊥y,∴x·y=0
即[a+(t2–3)b]·(–ka+tb)=0,整理后得
–ka2+[t–k(t2–3)]a·b+t(t2–3)·b2=0
∵a·b=0,a2=4,b2=1
∴上式化为–4k+t(t2–3)=0,∴k=
(3)解:讨论方程

于是f′(t)=

令f′(t)=0,解得t1=–1,t2=1.当t变化时,f′(t),f(t)的变化情况如下表:
当t=–1时,f(t)有极大值,f(t)极大值=
当t=1时,f(t)有极小值,f(t)极小值=–
而f(t)=


所以f(t)的图象大致如下:
于是当k>

当k=



解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析