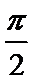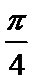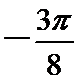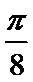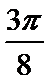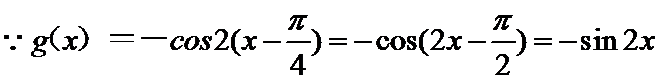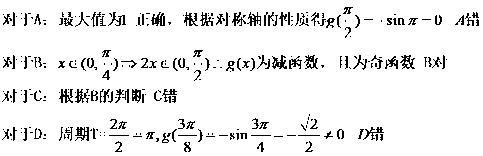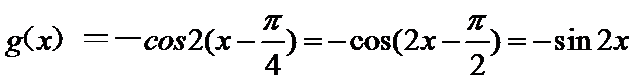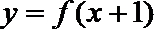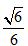- 余弦函数的图象
- 共11题
9.定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是 .
正确答案
7
知识点
8.将函数f(x)=-cos2x的图象向右
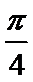
正确答案
解析
所以可以判断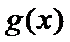
考查方向
解题思路
1)根据平移变换和诱导公式得到
2)根据三角函数的图像的性质对选项一一验证得出选项
易错点
主要易错于平移变换出错
知识点
21.若实数




(Ⅰ)若

(Ⅱ)已知函数






正确答案
(I)根据定义可得:

(Ⅱ)
解析
解析已在路上飞奔,马上就到!
知识点
12.定义在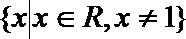
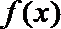

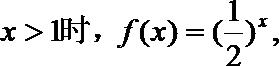
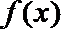
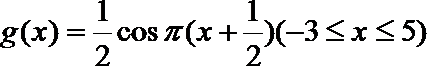
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 一艘轮船从O点正东100海里处的A点处出发,沿直线向O点正北100海里处的B点处航行.若距离O点不超过r海里的区域内都会受到台风的影响,设r是区间[50,100]内的一个随机数,则该轮船在航行途中会遭受台风影响的概率约为( )
正确答案
解析
由题意知O到距离斜边的距离为

考查方向
解题思路
画出示意图,找到距离斜边的距离为
易错点
本题不能将题目转化为所学的知识去解答。
知识点
已知函数
(1)求
(2)若
正确答案
见解析。
解析
(1)
所以最小正周期
由

故递减区间为
(2)由

由


故


所以实数

知识点
已知圆








正确答案
4
解析
这圆的圆心在原点,半径为5,圆心到直线



知识点
已知锐角△ABC的内角A,B,C的对边分别为a,b,c,23cos2A+cos 2A=0,a=7,c=6,则b=( )。
正确答案
解析
由23cos2A+cos 2A=0,得cos2A=
∵A∈

∵cos A=

故选D.
知识点
已知函数

(1)求函数
(2)如果



正确答案
(1)
解析
(1)

(2)


所以函数


故函数

知识点
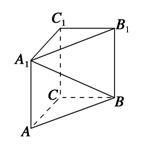
如图,在直三棱柱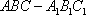
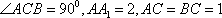
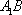
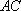
正确答案
解析
略
知识点
扫码查看完整答案与解析