- 三角函数中的恒等变换应用
- 共286题
已知复数
(1)求
(2)设





正确答案
(1)
解析
(1)∵
∴

∴当


(2)∵
∴
∴
将函数

把函数


∴
知识点
已知函数

(1)求

(2)求函数

正确答案
(1)1;
(2)
解析

(1)
显然,函数

(2)令


又因为

函数


知识点
设函数

(1)若


(2)若




正确答案
见解析。
解析
(1)
当

而


此时



∴


(2)依题意


整理,得
又


而





知识点
设





(1)求实数

(2)
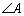




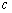



正确答案
见解析。
解析
(1)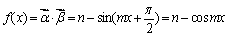
因为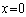
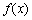
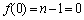
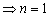
易知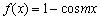

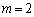

(2)由(Ⅰ)可知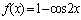
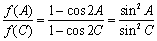
由正弦定理及余弦定理有: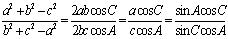
故
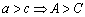
于是
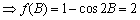
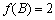
知识点
已知函数
(1)求
(2)求

正确答案
(1)
(2)
解析
(1)


∴函数

由 

得 
∴


(2)





知识点
扫码查看完整答案与解析















