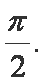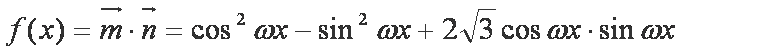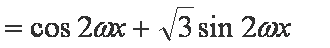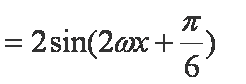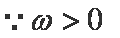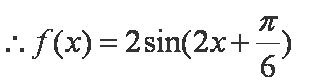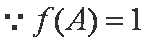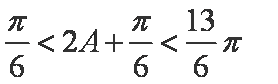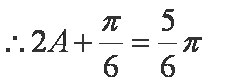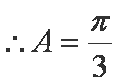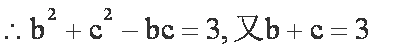- 三角函数中的恒等变换应用
- 共286题
现有4名教师参加说题比赛,共有4道备选题目,若每位选手从中有放回地随机选出一道题进行说题,其中恰有一道题没有被这4位选中的情况有
正确答案
解析
首先选择题目,从4道题目中选出3道,选法为



知识点
已知函数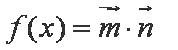
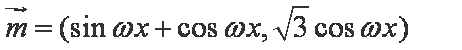
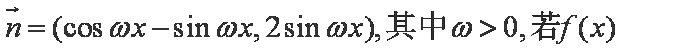
(1)求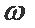
(2)在
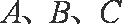
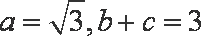
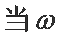
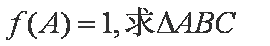
正确答案
见解析
解析
解析:(1)
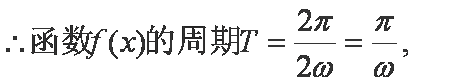
解得
(2)由(1)可知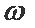

由余弦定理知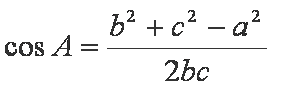
联立解得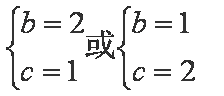
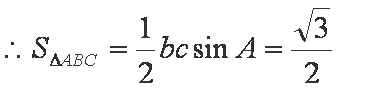
知识点
已知函数
(1)求函数

(2)求函数
正确答案
见解析。
解析
(1)
令 
函数


(2) 由
得: 
故
知识点
将函数f(x)=


正确答案
解析
将f(x)=sin 2x-cos 2x=2sin(2x-)的图象向左平移m个单位,得函数g(x)=2sin(2x+2m-)的图象,则由题意得2×+2m-=kπ+(k∈Z),即有m=+(k∈Z),∵m>-,∴当k=-1时,mmin=-.
知识点
如图,在圆







(1)当点



(2)若圆





正确答案
见解析
解析
本小题考查椭圆的标准方程与性质、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想等。
(1)设





即点


(2)解法一:
(i) 当直线




(ii)当直线


因为直线



又直线



所以直线


由




综上(i)(ii)知,直线

解法二 :设


(i)当





(ii)当



令



所以直线


由





综上(i)(ii)知,直线

知识点
扫码查看完整答案与解析