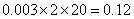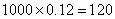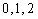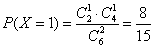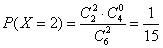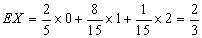- 统计与统计案例
- 共483题
A、B、C三个班共有100名学生,为调查他们的体育锻炼情况,通过分层抽样获得了部分学生一周的锻炼时间,数据如下表(单位:小时);
17.试估计C班的学生人数;
18.从A班和C班抽出的学生中,各随机选取一人,A班选出的人记为甲,C班选出的人记为乙,假设所有学生的锻炼时间相对独立,求该周甲的锻炼时间比乙的锻炼时间长的概率;
19.再从A、B、C三个班中各随机抽取一名学生,他们该周的锻炼时间分别是7,9,8.25(单位:小时),这3个新数据与表格中的数据构成的新样本的平均数记



正确答案
(1)40;
解析
(1)由已知可得,抽出的20名学生中,来自C班的学生有8名,根据分层抽样方法,C班的学生
考查方向
解题思路
(Ⅰ)根据图表判断C班人数,由分层抽样的抽样比计算C班的学生人数;
(Ⅱ)根据题意列出“该周甲的锻炼时间比乙的锻炼时间长”的所有事件,由独立事件概率公式求概率.
(Ⅲ)根据平均数公式进行判断即可.
易错点
运用逆向思维的方法(正难则反)求解,应用此公式时,一定要分清事件的对立事件到底是什么事件,不能重复或遗漏.
正确答案
(2)
解析
考查方向
解题思路
(Ⅰ)根据图表判断C班人数,由分层抽样的抽样比计算C班的学生人数;
(Ⅱ)根据题意列出“该周甲的锻炼时间比乙的锻炼时间长”的所有事件,由独立事件概率公式求概率.
(Ⅲ)根据平均数公式进行判断即可.
易错点
运用逆向思维的方法(正难则反)求解,应用此公式时,一定要分清事件的对立事件到底是什么事件,不能重复或遗漏.
正确答案
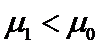
解析
考查方向
解题思路
(Ⅰ)根据图表判断C班人数,由分层抽样的抽样比计算C班的学生人数;
(Ⅱ)根据题意列出“该周甲的锻炼时间比乙的锻炼时间长”的所有事件,由独立事件概率公式求概率.
(Ⅲ)根据平均数公式进行判断即可.
易错点
运用逆向思维的方法(正难则反)求解,应用此公式时,一定要分清事件的对立事件到底是什么事件,不能重复或遗漏.
4.为了解某社区居民的家庭年收入所年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
根据上表可得回归直线方程

正确答案
解析
由已知得




考查方向
解题思路
由题意可知X平均和y平均,可得回归方长,把X=15代入方程求得y值即可。
易错点
线性回归方程列错,计算能力弱
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
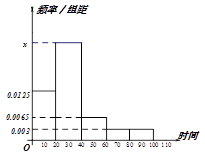
某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是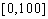
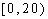
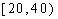
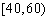
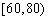
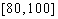
(1)求直方图中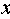
(2)如果上学路上所需时间不少于60分钟的学生可申请在学校住宿,请估计学校1000名新生中有多少名学生可以申请住宿;
(3)现有6名上学路上时间小于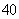
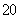
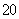
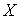
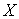
正确答案
见解析。
解析
(1)由直方图可得:
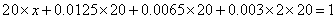
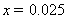
(2)新生上学所需时间不少于60分钟的频率为:
因为
所以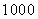
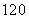
(3)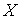
所以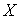
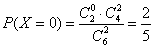
所以
知识点
今年年初,我国多个地区发生了持续性大规模的雾霾天气,给我们的身体健康产生了巨大的威胁。私家车的尾气排放也是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力。为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
[来源:学。科。网]
(1)完成被调查人员的频率分布直方图;
(2)若从年龄在


正确答案
见解析
解析
知识点
在某批次的某种灯泡中,随机地抽取200个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下. 根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于500天的灯泡是优等品,寿命小于300天的灯泡是次品,其余的灯泡是正品.
(1)根据频率分布表中的数据,写出a,b的值;
(2)某人从灯泡样品中随机地购买了
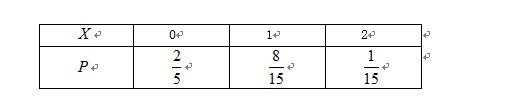
(3)某人从这个批次的灯泡中随机地购买了3个进行使用,若以上述频率作为概率,用X表示此人所购买的灯泡中次品的个数,求X的分布列和数学期望.
正确答案
见解析
解析
(1)解:

(2)解:由表可知:灯泡样品中优等品有50个,正品有100个,次品有50个,所以优等品、正品和次品的比例为



(3)解:


从本批次灯泡中购买3个,可看成3次独立重复试验,
所以



所以随机变量


(注:写出


知识点
一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如下图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在
正确答案
25
解析
略
知识点
国家对空气质量的分级规定如下表:
某市去年6月份30天的空气污染指数的监测数据如下:
根据以上信息,解决下列问题:
(1)写出下面频率分布表中
(2)某人计划今年




正确答案
见解析
解析
(1)解:
(2)解:由题意,该市4月份空气质量为优或良的概率为




…………………………,11分


知识点
10.某农户计划种植黄瓜和韭菜,种植面积不超过50亩,投入资金
为使一年的种植总利润(总利润=总销售收入-总种植成本)最大,那么黄瓜和韭菜
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.某中学初中部共有110名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析