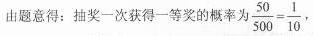- 统计与统计案例
- 共483题
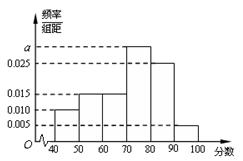
某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示),则分数在[70,80)内的人数是________。
正确答案
30
解析
略
知识点
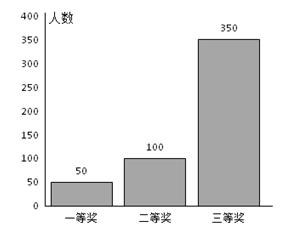
某超市进行促销活动,规定消费者消费每满100元可抽奖一次.抽奖规则:从装有三种只有颜色不同的球的袋中随机摸出一球,记下颜色后放回,依颜色分为一、二、三等奖,一等奖奖金15元,二等奖奖金10元,三等奖奖金5元.活动以来,中奖结果统计如图所示:
消费者甲购买了238元的商品,准备参加抽奖.以频率作为概率,解答下列各题。
(1)求甲恰有一次获得一等奖的概率;
(2)求甲获得20元奖金的概率;
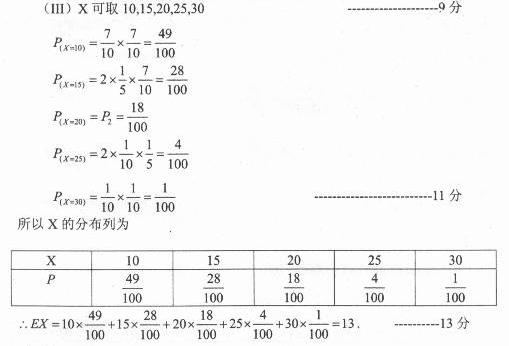
(3)记甲获得奖金金额为X,求X的分布列及期望EX.
正确答案
见解析
解析
知识点
随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是: 



(1)求样本的人数及x的值;
(2)估计样本的众数,并计算频率分布直方图中
(3)从成绩不低于80分的样本中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为

正确答案
见解析。
解析
(1)由题意得,分数在

所以样本人数为


(2)从分组区间和频数可知,样本众数的估计值为
由(1)知分数在
所以频率分布直方图中
(3)成绩不低于80分的样本人数为4+2=6(人),成绩在90分以上(含90分)的人数为




所以
所以
知识点
右图是一容量为
正确答案
解析
略
知识点
如图是某班50位学生期中考试数学成绩的频率分布直方图,其中成绩分组区间是:






正确答案
解析
略
知识点
执行如图所示的程序框图,输出的T= 。
正确答案
29
解析
略
知识点
已知一个样本容量为
正确答案
15,75
解析
略
知识点
将容量为




正确答案
解析
略
知识点
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克),重量的分组区间为


(1)根据频率分布直方图,求重量超过505克的产品数量;
(2)在上述抽取的40个产品中任职2件,设

(3)从流水线上任取5件产品,估计其中恰有2件产品的重量超过505克的概率。
正确答案
见解析
解析
(1)重量超过505克的产品数量是
(2)




-------------------------------------------------------9分
(3)由(1)的统计数据知,抽取的40件产品中有12件产品的重量超过505克,其频率为



故所求的概率为
知识点
某校高二年级进行社会实践,对[25, 55]岁的人群随机抽取n个人进行了一次是否开通“微信”, 若开通“微信”的为“时尚族”,否则称为“非时尚族”,通过调查分别得到如图1所示统计表,如图2所示各年龄段人数频率分布直方图:
请完成以下问题:
(1)补全频率直方图,并求n,a,p的值;
(2)从[40,45)岁和[45,50)岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络“时尚达人”大赛,其中选取3人作为领队,记选取的3名领队中年龄在[40,45)岁得人数为ξ,求ξ的分布列和数学期望E(X).
正确答案
见解析
解析
(1)第二组的频率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3,所以高为
第一组的人数为
频率为0.04×5=0.2,所以
第四组的频率为0.03×5=0.15,人数为1000×0.15=150,
(2)因为[40,45)岁与[45,50)岁年龄段的“时尚族”的比值为60:30=2:1,所以分层抽样法抽取18人,[40,45)岁中有12人,[45,50)岁中有6人,随机变量





数学期望为
知识点
扫码查看完整答案与解析