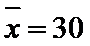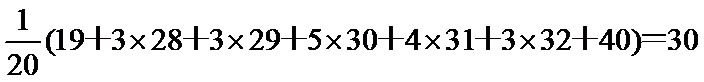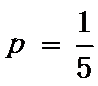- 统计与统计案例
- 共483题
某车间20名工人年龄数据如下表:
21.求这20名工人年龄的众数与平均数;
22.以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
23.从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率。
正确答案
众数是30;
解析
(Ⅰ) 由题意可知,这20名工人年龄的众数是30,
这20名工人年龄的平均数为
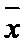
考查方向
解题思路
根据众数和平均数的定义,即可得出;
易错点
熟记众数和平均数的概念.
正确答案
见解析
解析
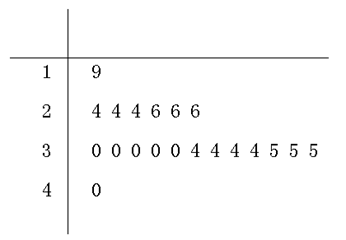
这20名工人年龄的茎叶图如图所示:
考查方向
解题思路
根据画茎叶图的步骤,画图即可;
易错点
无
正确答案
解析
记年龄为24岁的三个人为A1,A2,A3;年龄为26岁的三个人为B1,B2,B3则从这6人中随机抽取2人的所有可能为
{A1,A2},{A1,A3},{A2,A3},{A1,B1},{A1,B2},
{A1,B3},{A2,B1},{A2,B2},{A2,B,3},{A3,B1},
{A3,B2},{A,3,B3},{B1,B2},{B1,B3},{B2,B3}共15种。
满足题意的有{A1,A2},{A1,A3},{A2,A3}3种,
故所求的概率为P=
考查方向
解题思路
利用枚举法,将6人中随机抽取2人的所有可能的情况列举出来,再求概率.
易错点
古典概型中使用枚举时,要注意不重不漏.
某车间20名工人年龄数据如下表:
21.求这20名工人年龄的众数与平均数;
22.以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
23.从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率。
正确答案
众数是30;
解析
(Ⅰ) 由题意可知,这20名工人年龄的众数是30,
这20名工人年龄的平均数为

考查方向
解题思路
根据众数和平均数的定义,即可得出;
易错点
熟记众数和平均数的概念.
正确答案
见解析
解析
这20名工人年龄的茎叶图如图所示:
考查方向
解题思路
根据画茎叶图的步骤,画图即可;
易错点
无
正确答案
解析
记年龄为24岁的三个人为A1,A2,A3;年龄为26岁的三个人为B1,B2,B3则从这6人中随机抽取2人的所有可能为
{A1,A2},{A1,A3},{A2,A3},{A1,B1},{A1,B2},
{A1,B3},{A2,B1},{A2,B2},{A2,B,3},{A3,B1},
{A3,B2},{A,3,B3},{B1,B2},{B1,B3},{B2,B3}共15种。
满足题意的有{A1,A2},{A1,A3},{A2,A3}3种,
故所求的概率为P=
考查方向
解题思路
利用枚举法,将6人中随机抽取2人的所有可能的情况列举出来,再求概率.
易错点
古典概型中使用枚举时,要注意不重不漏.
正确答案
LUE
知识点
正确答案
略
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
样本(x1,x2,…,xn)的平均数为



正确答案
解析
由已知,得x1+x2+…+xn=


整理,得
∵
∴αm+(α-1)n=0,即
又


又n,m∈N+,∴n<m.
知识点
为了考察某校各班参加课外书法小组的人数,从全校随机抽取5个班级,把每个班级参加该小组的人数作为样本数据,已知样本平均数为7,样本方差为4,且样本数据互不相同,则样本数据中的最大值为__________。
正确答案
10
解析
设5个班级的人数分别为x1,x2,x3,x4,x5,则
=4,
即5个整数平方和为20,最大的数比7大不能超过3,否则方差超过4,故最大值为10,最小值为4
知识点
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取
本,称出它们的重量(单位:克),重量分组区间为



由此得到样本的重量频率分布直方图,如图
(1)求
(2)根据样本数据,试估计盒子中小球重量的平均值;
(注:设样本数据第



则样本数据的平均值为
(3)从盒子中随机抽取



正确答案
见解析。
解析
(1) 解:由题意,得
解得
(2)解:

由样本估计总体,可估计盒子中小球重量的平均值约为
(3)解:利用样本估计总体,该盒子中小球重量在








∴
∴
(或者
知识点
贵阳市某中学高三(2)班排球队和篮球队各有10名同学,现测得排球队10人的身高(单位:cm)分别是:162,170,171,182,163,158,179,168,183,168,篮球队10人的身高(单位:cm)分别是:170,159,162,173,181,165,176,168,178,179.
19.请把两队身高数据记录在图中所示的茎叶图中,并求出两个队的身高的平均数;
20.现从两队所在身高超过178cm的同学中随机抽取三名同学,则恰好两人来自排球队一人来自篮球队的概率是多少?
正确答案
(Ⅰ)画出茎叶图如图2.
图2
…………………………………………………………………(2分)



解析
(Ⅰ)画出茎叶图如图2.
图2
…………………………………………………………………(2分)


考查方向
主要考茎叶图和平均数的计算。
解题思路
根据茎叶图的定义画出茎叶图,根据公式计算平均数。
易错点
公式记错,算平均数时计算错误。
教师点评
此题着手点低,代入公式即可解决问题。
正确答案
(Ⅱ)两队所有身高超过178cm的学生共有5人,
其中3人来自排球队记为a,b,c,2人来自篮球队记为A,B,
则从5人中抽取3名学生的基本事件

其中恰好2人来自排球队1人来自篮球队的事件为{a,b,A},{a,b,B},{a,c,A},{a,c,B},{b,c,A},{b,c,B},共6个,
∴恰好2人来自排球队1人来自篮球队的概率
解析
(Ⅱ)两队所有身高超过178cm的学生共有5人,
其中3人来自排球队记为a,b,c,2人来自篮球队记为A,B,
则从5人中抽取3名学生的基本事件

其中恰好2人来自排球队1人来自篮球队的事件为{a,b,A},{a,b,B},{a,c,A},{a,c,B},{b,c,A},{b,c,B},共6个,
∴恰好2人来自排球队1人来自篮球队的概率
考查方向
本题主要考查简单随机抽样的概率问题。
解题思路
应用简单随机抽样的方法,一一列举出来,便解决问题。
易错点
在写随机事件的中数的时候容易漏写或多写。
教师点评
本题主要考查了随机事件的概率问题及简单的随机抽样。
18.(本题满分12分)
某公司为了解用户对其产品的满意度,从

A地区:62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
B地区:73 83 62 51 91 46 53 73 64 82
93 48 65 81 74 56 54 76 65 79
(Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,得出结论即可);
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
记时间C:“A地区用户的满意度等级高于B地区用户的满意度等级”.假设两地区用户的评价结果相互独立.根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率.
正确答案
(Ⅰ)详见解析;(Ⅱ)
试题分析:(Ⅰ)将
(Ⅱ)事件“A地区用户的满意度等级高于B地区用户的满意度等级”分为两种情况:当B地区满意度等级为不满意时,A地区的满意度等级为满意或非常满意;当B地区满意度等级为满意时,A地区满意度等级为非常满意.再利用互斥事件和独立事件的概率来求解.
试题(Ⅰ)两地区用户满意度评分的茎叶图如下

则







由所给数据得












解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析