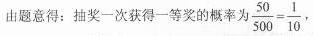- 频率分布直方图
- 共93题
今年年初,我国多个地区发生了持续性大规模的雾霾天气,给我们的身体健康产生了巨大的威胁。私家车的尾气排放也是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力。为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
[来源:学。科。网]
(1)完成被调查人员的频率分布直方图;
(2)若从年龄在


正确答案
见解析
解析
知识点
如图是根据某班学生在一次数学考试中的成绩画
出的频率分布直方图,若80分以上为优秀,根据
图形信息可知:这次考试的优秀率为 ( )
正确答案
解析
略
知识点
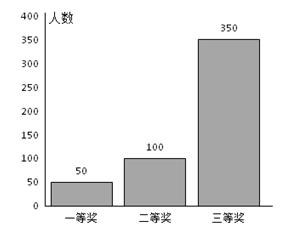
某超市进行促销活动,规定消费者消费每满100元可抽奖一次.抽奖规则:从装有三种只有颜色不同的球的袋中随机摸出一球,记下颜色后放回,依颜色分为一、二、三等奖,一等奖奖金15元,二等奖奖金10元,三等奖奖金5元.活动以来,中奖结果统计如图所示:
消费者甲购买了238元的商品,准备参加抽奖.以频率作为概率,解答下列各题。
(1)求甲恰有一次获得一等奖的概率;
(2)求甲获得20元奖金的概率;
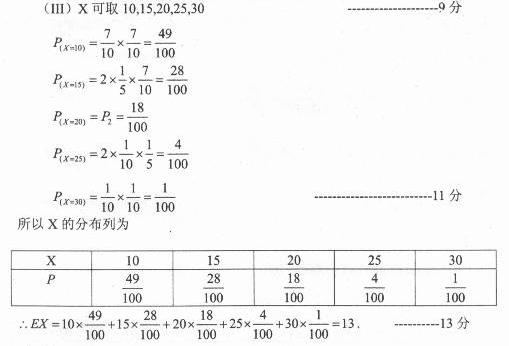
(3)记甲获得奖金金额为X,求X的分布列及期望EX.
正确答案
见解析
解析
知识点
随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是: 



(1)求样本的人数及x的值;
(2)估计样本的众数,并计算频率分布直方图中
(3)从成绩不低于80分的样本中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为

正确答案
见解析。
解析
(1)由题意得,分数在

所以样本人数为


(2)从分组区间和频数可知,样本众数的估计值为
由(1)知分数在
所以频率分布直方图中
(3)成绩不低于80分的样本人数为4+2=6(人),成绩在90分以上(含90分)的人数为




所以
所以
知识点
右图是一容量为
正确答案
解析
略
知识点
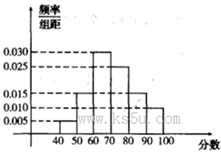
某校高一年级60名学生参加数学竞赛,成绩全部在40分至100分之间,现将成绩分成以下6段:
(1)求成绩在区间
(2)从成绩大于等于80分的学生中随机选3名学生,其中成绩在[90,100]内的学生人数为ξ,求ξ的分布列与均值.
正确答案
见解析。
解析
解:(1)因为各组的频率之和为1,所以成绩在区间

(2)由已知和(1)的结果可知成绩在区间

成绩在区间

依题意,ξ可能取的值为0,1,2,3
所以ξ的分布列为
则均值Eξ=
知识点
已知一个样本容量为
正确答案
15,75
解析
略
知识点
某市规定,高中学生三年在校期间参加不少于






(1)求抽取的


(2)从全市高中学生(人数很多)中任意选取





正确答案
见解析
解析
(1)根据题意,
参加社区服务时间在时间段

参加社区服务时间在时间段

所以抽取的200位学生中,参加社区服务时间不少于90小时的学生人数为
所以从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的
概率估计为
(2)由(1)可知,从全市高中生中任意选取1人,其参加社区服务时间不少于90小时的概率为
由已知得,随机变量

所以



随机变量
因为 


知识点
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生500名,据此估计,该模块测试成绩不少于60分的学生人数为_________。
正确答案
400
解析
略
知识点
某校高二年级进行社会实践,对[25, 55]岁的人群随机抽取n个人进行了一次是否开通“微信”, 若开通“微信”的为“时尚族”,否则称为“非时尚族”,通过调查分别得到如图1所示统计表,如图2所示各年龄段人数频率分布直方图:
请完成以下问题:
(1)补全频率直方图,并求n,a,p的值;
(2)从[40,45)岁和[45,50)岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络“时尚达人”大赛,其中选取3人作为领队,记选取的3名领队中年龄在[40,45)岁得人数为ξ,求ξ的分布列和数学期望E(X).
正确答案
见解析
解析
(1)第二组的频率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3,所以高为
第一组的人数为
频率为0.04×5=0.2,所以
第四组的频率为0.03×5=0.15,人数为1000×0.15=150,
(2)因为[40,45)岁与[45,50)岁年龄段的“时尚族”的比值为60:30=2:1,所以分层抽样法抽取18人,[40,45)岁中有12人,[45,50)岁中有6人,随机变量





数学期望为
知识点
扫码查看完整答案与解析