- 频率分布直方图
- 共93题
某学校为了解高三年级学生寒假期间的学习情况,抽取甲、乙两班,调查这两个班的学生在寒假期间每天平均学习的时间(单位:小时),统计结果绘成频率分布直方图(如图),已知甲、乙两班学生人数相同,甲班学生每天平均学习时间在区间
(1)求直方图中

(2)从甲、乙两个班每天平均学习时间大于




正确答案
见解析
解析
(1)由直方图知,

因为甲班学习时间在区间

所以甲班的学生人数为

所以甲班学习时间在区间

(2)乙班学习时间在区间

由(1)知甲班学习时间在区间

在两班中学习时间大于







所以随机变量

知识点
某中学从某次考试成绩中抽取若干名学生的分数,并绘制
成如图1的频率分布直方图,样本数据分组为




样的方法从样本中抽取分数在
则其中分数在
正确答案
解析
略
知识点
某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况,随机抽查了该市当天
若网购金额超过

义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为
(1)试确定



(2)该营销部门为了进一步了解这
达人”中用分层抽样的方法确定





正确答案
见解析。
解析
(1)根据题意,有
解得


补全频率分布直方图如图所示。
(2)用分层抽样的方法,从中选取
其中“网购达人”有

故




所


知识点
在样本的频率分布直方图中,一共有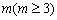

正确答案
解析
略。
知识点
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取
本,称出它们的重量(单位:克),重量分组区间为



由此得到样本的重量频率分布直方图,如图
(1)求
(2)根据样本数据,试估计盒子中小球重量的平均值;
(注:设样本数据第



则样本数据的平均值为
(3)从盒子中随机抽取



正确答案
见解析。
解析
(1) 解:由题意,得
解得
(2)解:

由样本估计总体,可估计盒子中小球重量的平均值约为
(3)解:利用样本估计总体,该盒子中小球重量在








∴
∴
(或者
知识点
扫码查看完整答案与解析










