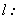- 区间与无穷的概念
- 共9题
对于定义域为












27. 验证

28. 设



29. 证明:“







正确答案
(1)略.
解析
试题分析:(1)根据余弦周期函数的定义,判断cosg(x+6π)是否等于cosg(x)即可.
证明:(1)易见

对任意

所以
即

考查方向
解题思路
新定义问题一般先考察对周期定义的理解
易错点
周期定义的理解运用
正确答案
(2)略
解析
试题分析:(2)根据f(x)的值域为R,便可得到存在x0,使得f(x0)=c,而根据f(x)在R上单调递增即可说明x0∈[a,b],从而完成证明;
(2)由于





若







考查方向
解题思路
新定义问题一般先考察对定义的理解,这时只需一一验证定义中各个条件即可.二是考查满足新定义的函数的简单应用,如在某些条件下,满足新定义的函数有某些新的性质,这也是在新环境下研究“旧”性质,此时需结合新函数的新性质,探究“旧”性质.三是考查综合分析能力,主要将新性质有机应用在“旧”性质,创造性证明更新的性质.
易错点
存在性问题与函数单调性最值的联系
正确答案
(3)略
解析
试题分析:(3)只需证明u0+T为方程cosf(x)=1在区间[T,2T]上的解得出u0为方程cosf(x)=1在[0,T]上的解,是否为方程的解,带入方程,使方程成立便是方程的解.证明对任意x∈[0,T],都有f(x+T)=f(x)+f(T),可讨论x=0,x=T,x∈(0,T)三种情况:x=0时是显然成立的;x=T时,可得出cosf(2T)=1,从而得到f(2T)=2k1π,k1∈Z,根据f(x)单调递增便能得到k1>2,然后根据f(x)的单调性及方程cosf(x)=1在[T,2T]和它在[0,T]上解的个数的情况说明k1=3,和k1≥5是不存在的,而k1=4时结论成立,这便说明x=T时结论成立;而对于x∈(0,T)时,通过考查cosf(x)=c的解得到f(x+T)=f(x)+f(T),综合以上的三种情况,最后得出结论即可.
(3)若








同理,若




以下证明最后一部分结论.
由(2)所证知存在






而





与之前类似地可以证明:





从而


故





对于


而

类似地,当




结论成立.
考查方向
解题思路
新定义问题一般先考察对定义的理解,这时只需一一验证定义中各个条件即可.二是考查满足新定义的函数的简单应用,如在某些条件下,满足新定义的函数有某些新的性质,这也是在新环境下研究“旧”性质,此时需结合新函数的新性质,探究“旧”性质.三是考查综合分析能力,主要将新性质有机应用在“旧”性质,创造性证明更新的性质.
易错点
周期定义的理解运用;存在性问题与函数单调性最值的联系;任意性问题成立的条件判断
22. 已知函数
(1)求
(2)设不等式

正确答案
(1)
令
从而
在
所以,当x=0时,
(2)因为不等式
且
所以对于任意

由
当x=0时,上述不等式显然成立,故只需考虑
将
令
令
从而
所以,当

解析
解析已在路上飞奔,马上就到!
知识点
凡事都有度,对于适当的超前,还是有必要的。但是现在的幼师,甚至校长都可能对幼儿教育一窍不通,把幼儿教育商业化,这难免违背了教育幼儿的初衷。他们的教育完全是迎合一些“望子成龙”的家长的需求。所以,在这件事情上,幼儿园负有部分责任,而家长也起着推波助澜的作用。 本段文字主要说明( )。
A.现在的幼儿教育过于超前
B.幼儿教育商业化违背教育初衷
C.幼儿教育违背初衷,幼儿园、家长难辞其咎
D.幼儿教育者的素质有待提高
正确答案
C
解析
[解析] 主旨概括题。通过阅读可以很快把重心锁定在最后一句话,在幼儿教育过于商业化而违背初衷的问题上幼儿园和家长都负有责任,这是作者的结论性语句。因此本题正确答案选择C项。A、B、D三项表述无误.但都是次要观点。

正确答案
80
解析
略
知识点
已知函数
(1)求
(2)求

正确答案
(1)

(2)最大值2,最小值1
解析
(1)由


故


因为

所以

(2)由 
当
当
知识点
方程

正确答案
4
解析
略
知识点
已知直线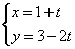
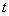
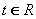


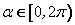
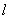
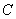
正确答案
(1,3)
解析
略
知识点
在复平面内,复数
正确答案
解析
略
知识点
对具有线性相关关系的变量x,y,有一组观测数据(



正确答案
解析
略
知识点
扫码查看完整答案与解析