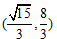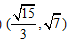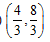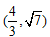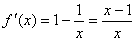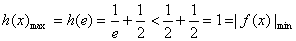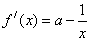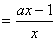- 函数解析式的求解及常用方法
- 共177题
已知以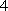
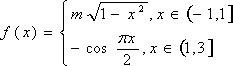
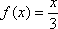
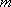
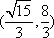
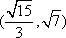
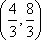
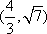
正确答案
解析
略
知识点
某种型号汽车四个轮胎半径相同,均为
















(1)如图(2)所示,


求证:
(2)当



正确答案
见解析
解析
解析:(1)由OE//BC,OH//AB,得∠EOH=

Rt


∠BOM=
在Rt


(2)由(1)结论得OE=
设OH=x,OF=y,
在
2802=x2+(

解得x
在
2802=y2+(

解得y

所以,FH=y-x
即后轮中心从F处移动到H处实际移动了约98cm.
知识点
科学研究表明:一般情况下,在一节40分钟的课中,学生的注意力随教师讲课的时间变化而变化。开始上课时,学生的注意力逐步增强,随后学生的注意力开始分散。经过实验分析,得出学生的注意力指数

(1)如果学生的注意力指数不低于80,称为“
(2)现有一道数学压轴题,教师必须持续讲解24分钟,为了使效果更好,要求学生的注意力指数在这24分钟内的最低值达到最大,那么,教师上课后从第几分钟开始讲解这道题?(精确到1分钟)
正确答案
(1)

解析
解析:(1)由于学生的注意力指数不低于80,即
当


当


所以
故学生处于“理想听课状态”所持续的时间有
(2)设教师上课后从第
所以
要学生的注意力指数最低值达到最大,只需
即
解得
所以,教师上课后从第
知识点
设







正确答案
解析
略
知识点
已知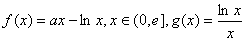
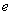
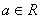
(1)讨论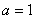
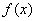
(2)求证:在(1)的条件下,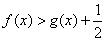
(3)是否存在实数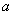
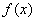
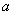
正确答案
见解析
解析
(1)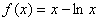
∴当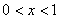
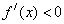
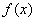
当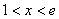
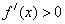
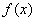
∴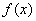
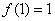
(2)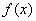
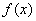
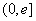
∴ 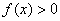
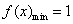
令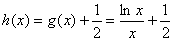
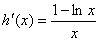
当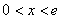
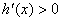
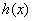
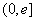
∴
∴在(1)的条件下,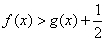
(3)假设存在实数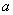
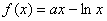
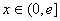
① 当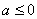
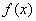
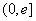
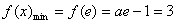
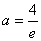
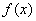
② 当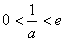
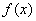
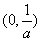
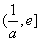
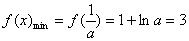
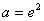
③ 当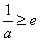
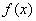
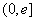
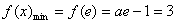
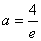
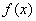
综上,存在实数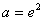
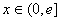
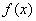
知识点
扫码查看完整答案与解析