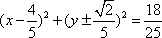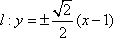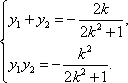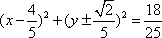· 圆锥曲线的综合问题

· 直线、圆及圆锥曲线的交汇问题

直线、圆及圆锥曲线的交汇问题
共97题

· 圆锥曲线的综合问题

· 直线、圆及圆锥曲线的交汇问题

直线、圆及圆锥曲线的交汇问题
共97题

热门试卷

X 查看更多试卷

1

题型：简答题

|

简答题 · 12 分

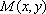
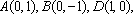
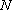
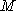
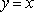
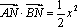
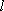
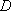
在平面直角坐标系中，已知动点，点点与点关于直线对称，且.直线是过点的任意一条直线。

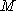
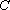
（1）求动点所在曲线的轨迹方程；

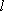
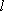
（2）设直线与曲线交于两点，且，求直线的方程；

（3）设直线与曲线交于两点，求以的长为直径且经过坐标原点的圆的方程。

正确答案

（1）（2）（3）

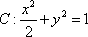
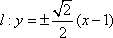
解析

（1）依据题意，可得点.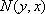

，

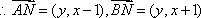
又，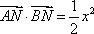

.

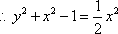
所求动点的轨迹方程为.

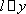
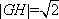
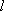
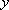
（2）若直线轴，则可求得，这与已知矛盾，因此满足题意的直线不平行于轴。

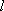
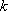
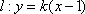
设直线的斜率为，则。

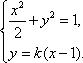
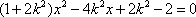
由得。

设点，有且恒成立（因点在椭圆内部）。

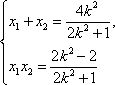
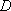
又，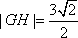

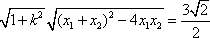
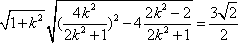
于是，，即，

解得。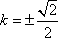

所以，所求直线

（3）当直线轴时，，点到圆心的距离为1.即点在圆外，不满足题意.

满足题意的直线的斜率存在，设为，则.

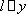
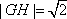
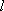
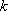
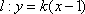
设点，由（2）知，进一步可求得

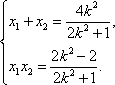
依据题意，有，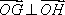

，

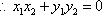
即，解得.

所求圆的半径，

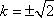
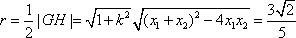
圆心为.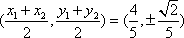

所求圆的方程为：

知识点

直线的一般式方程直线与圆锥曲线的综合问题直接法求轨迹方程直线、圆及圆锥曲线的交汇问题

1

题型：单选题

|

单选题 · 5 分

已知双曲线的离心率为2，一个焦点与抛物线的焦点相同，则双曲

线的渐近线方程为

A

B

C

D

正确答案

A

解析

略

知识点

直线、圆及圆锥曲线的交汇问题

1

题型：简答题

|

简答题 · 12 分

如图，已知椭圆：的离心率为，以椭圆的左顶点为圆心作圆：，设圆与椭圆交于点与点。

（1）求椭圆的方程；

（2）求的最小值，并求此时圆的方程；

（3）设点是椭圆上异于,的任意一点，且直线分别与轴交于点，为坐标原点，求证：为定值，

正确答案

见解析。

解析

（1）

故椭圆的方程为，

（2）点与点关于轴对称，设，，不妨设。

由于点在椭圆上，所以，（*）

由已知，则，，

。

由于，故当时，取得最小值为。

由（*）式，，故，又点在圆上，代入圆的方程得到，

故圆的方程为：，

（3）

知识点

向量在几何中的应用圆的标准方程椭圆的定义及标准方程直线与圆锥曲线的综合问题直线、圆及圆锥曲线的交汇问题

1

题型：填空题

|

填空题 · 5 分

以抛物y2＝4x的焦点为圆心且与双曲线的渐近线相切的圆的方程

是＿＿＿＿

正确答案

解析

略

知识点

圆的标准方程椭圆的几何性质抛物线的标准方程和几何性质直线、圆及圆锥曲线的交汇问题

1

题型：单选题

|

单选题 · 5 分

设点P是双曲线与圆在第一象限的交点，分别是双曲线的左、右焦点，且，则双曲线的离心率为（）

A

B2

C

D3

正确答案

A

解析

略。

知识点

双曲线的几何性质直线、圆及圆锥曲线的交汇问题

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 文科数学 > 直线、圆及圆锥曲线的交汇问题

扫码查看完整答案与解析