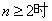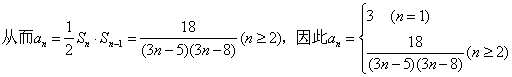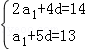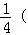- 导数的运算
- 共307题
已知函数f(x)的图象与函数h(x)=x++2的图象关于点A(0,1)对称。
(1)求f(x)的解析式;
(2)若g(x)=x2•[f(x)﹣a],且g(x)在区间[1,2]上为增函数,求实数a的取值范围。
正确答案
见解析。
解析
(1)设f(x)的图象上任一点P(x,y),
则点P关于点A(0,1)对称P′(﹣x,2﹣y)在h(x)的图象上,
∴2﹣y=﹣x﹣+2,得y=

(2)由(1)得,g(x)=x2•[f(x)﹣a]=x2•[
则g′(x)=3x2﹣2ax+1,
∵g(x)在区间[1,2]上为增函数,
∴3x2﹣2ax+1≥0在区间[1,2]上恒成立,
即a≤(
∵y=
则a≤
知识点
已知长方形ABCD,

(1)求以A,B为焦点,且过C,D两点的椭圆P的标准方程;
(2)已知定点E(—1,0),直线

正确答案
见解析
解析
(1)由题意可得点A,B,C的坐标分别为

设椭圆的标准方程是



(2)将



设



因为以



而



如果










知识点
在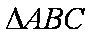
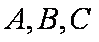
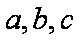
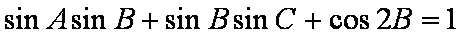
(1)求证: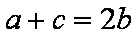
(2)若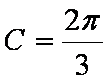
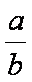
正确答案
见解析
解析
解:(1)由已知得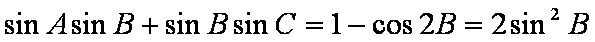
由正弦定理得: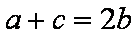
(2)由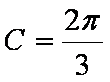
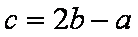
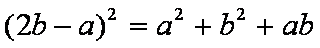
即有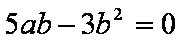
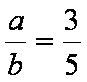
知识点
已知数列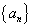
(1)求证:{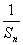
(2)求{a n }的通项公式;
(3)数列{an }中是否存在自然数k0,使得当自然数k≥k 0时使不等式a k>a k+1对任意大于等于k的自然数都成立,若存在求出最小的k值,否则请说明理由.
正确答案
见解析
解析
解析:(1)由已知当
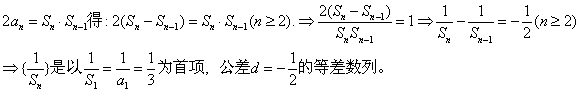
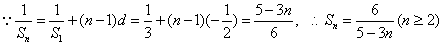
(3)
知识点
在某海湾为我国商船护航的甲、乙两驱逐舰分别在海面上A,B两点处正常巡航,甲舰位于乙舰北偏西25°方向的





正确答案
40
解析
设
在






在

由余弦定理得

解得

知识点
数列{an}的通项公式为an=n+,若对任意的n∈N*都有an≥a5,则实数b的取值范围是 。
正确答案
[20,30]
解析
由题意可得b>0,
∵对所有n∈N*不等式an≥a5恒成立,
∴

经验证,数列在(1,4)上递减,(5,+∞)上递增,
或在(1,5)上递减,(6,+∞)上递增,符合题意。
知识点
已知等差数列{an}满足:a2+a4=14,a6=13,{an}的前n项和为Sn。
(1)求an及Sn;
(2)令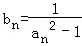
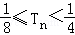
正确答案
见解析
解析
(1)解:设首项为a1,公差为d,则
∵a2+a4=14,a6=13,∴
∴a1=3,d=2
∴an=3+2(n﹣1)=2n+1,Sn=3n+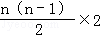
(2)证明: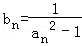
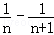
∴Tn=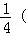
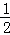
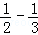
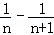
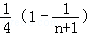
∵Tn单调递增,∴Tn≥T1=
∴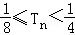
知识点
已知过抛物线




(1)求该抛物线的方程;
(2)



正确答案
(1)
解析
解析:(1)直线AB的方程是
所以:

抛物线方程为:
(2)由p=4,




设





知识点
已知



正确答案
解析
试题分析:作出不等式组







知识点
函数
正确答案
解析
x-2>0且x-2


知识点
扫码查看完整答案与解析