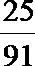导数的运算
共307题

· 导数的运算

导数的运算
共307题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

17．如图：在矩形ABCD中，AB＝5，BC＝3，沿对角线BD把△ABD折起，使A移到A1点，过点A1作A1O⊥平面BCD，垂足O恰好落在CD上。

（1）求证：BC⊥A1D；

（2）求直线A1B与平面BCD所成角的正弦值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

题型：单选题

单选题 · 5 分

7．若△的三个内角满足,则△（　　）

A一定是锐角三角形

B一定是直角三角形

C一定是钝角三角形

D可能是锐角三角形,也可能是钝角三角形

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

题型：填空题

填空题 · 5 分

15．对于三次函数f(x)＝ax3＋bx2＋cx＋d(a≠0)，定义：设f″(x)是函数y＝f(x)的导数y＝f′(x)的导数，若方程f″(x)＝0有实数解x0，则称点为函数y＝f(x)的“拐点”。有同学发现“任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心；且“拐点”就是对称中心.”请你根据这一发现，求：

（1）函数f(x)＝x3－3x2＋3x对称中心为___________；

（2）若函数，则=___________。

正确答案

（1，1）； 2010

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算利用导数求函数的极值分组转化法求和进行简单的合情推理

题型：单选题

单选题 · 5 分

12．已知为R上的可导函数，且满足，对任意正实数，下面不等式恒成立的是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算利用导数研究函数的单调性

题型：填空题

填空题 · 4 分

8．某足球队共有11名主力队员和3名替补队员参加一场足球比赛，其中有2名主力和1名替补队员不慎误服违禁药物，依照比赛规定，比赛后必须随机抽取2名队员的尿样化验，则能查到服用违禁药物的主力队员的概率为（）。（结果用分数表示）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

题型：简答题

简答题 · 12 分

17.如图，一个多面体的直观图如图所示，它的正视图和俯视图都是边长为2的正方形，左视图如图b所示。已知M、N分别是AF、BC的中点。

（1）求证：MN∥平面CDEF；

（2）求四棱锥E－ABCD的体积；

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

题型：单选题

单选题 · 5 分

9．函数的导函数是，若对任意的，都有成立，则（）

D无法比较

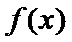
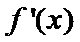
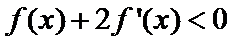
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算利用导数研究函数的单调性

题型：填空题

填空题 · 5 分

15．定义在区间上的函数，是函数的导数，如果，使得，则称为上的“中值点”。下列函数：

①

②，

③，

④。

其中在区间上的“中值点”多于一个的函数是___________（请写出你认为正确的所有结论的序号）

正确答案

①①

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

题型：简答题

简答题 · 10 分

21．已知：函数（其中常数、），是奇函数。

（1）求：的表达式；

（2）求：的单调性。

正确答案

（Ⅰ）由题意得。

因此。

因为函数是奇函数，所以，
　　即对任意实数x，有，
　　从而3a+1=0，b=0，解得，b=0，
　　因此的解析表达式为。
　　（Ⅱ）由（Ⅰ）知，所以，

令，解得，，
　　当或时，，
　　从而在区间，上是减函数；
　　当时，，从而在区上是增函数。
　　由前面讨论知，在区间[1，2]上的最大值与最小值只能在x=1，，2时取得，
　　而，，。
　　因此在区间[1，2]上的最大值为，最小值为。

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法导数的运算利用导数研究函数的单调性

题型：简答题

简答题 · 14 分

20．已知函数

（1）若，求的值；

（2）若对于恒成立，求实数的取值范围

正确答案

（1）当时，；当时，

由条件可知，即，

解得

，

（2）当时，

即．

，

故的取值范围是

解析

解析已在路上飞奔，马上就到！

知识点

指数幂的运算导数的运算不等式恒成立问题

继续学习学习下一知识点

下一知识点 : 导数的加法与减法法则

百度题库 > 高考 > 文科数学 > 导数的运算

扫码查看完整答案与解析