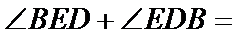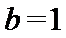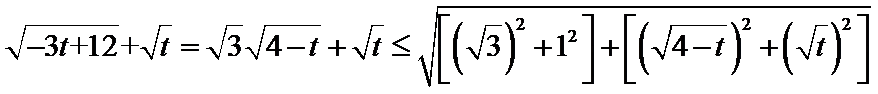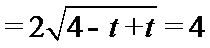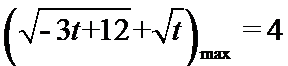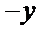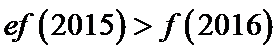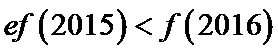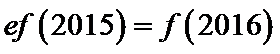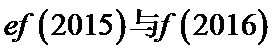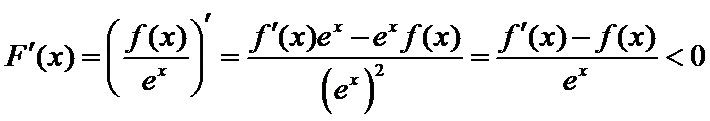- 导数的运算
- 共307题
函数
正确答案
2
知识点
已知函数
(I)当


(II)若当


正确答案
(I)






(II)当

令

(i)当





(ii)当


由







综上,
知识点
选修4-1:几何证明选讲(请回答27,28题)
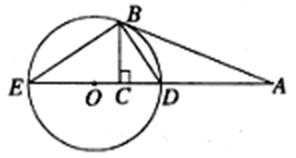
如图,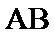

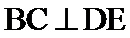
选修4-4:坐标系与参数方程(请回答29/30题)
在直角坐标系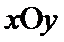
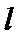
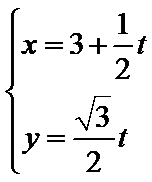
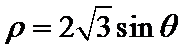
选修4-5:不等式选讲(请回答31,32题)
已知关于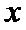
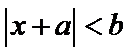
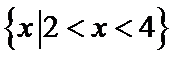
27.证明: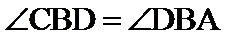
28.若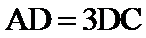
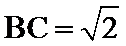
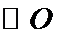
29.写出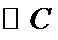
30.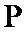
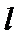
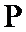
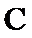
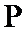
31.求实数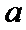
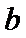
32.求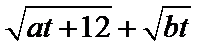
正确答案
(Ⅰ)因为

又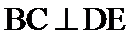
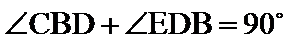
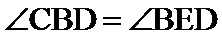
又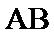
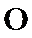
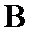
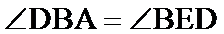
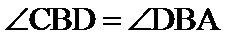
解析
试题分析: (Ⅰ)先证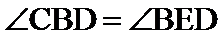
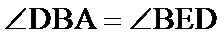
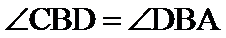
考查方向
解题思路
解题时一定要注意灵活运用圆的性质,否则很容易出现错误.
易错点
灵活运用圆的性质;长度计算时
正确答案
(Ⅱ)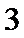
解析
试题分析:(Ⅱ)先由(Ⅰ)知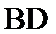

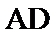
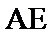
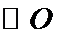
(Ⅱ)由(Ⅰ)知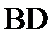

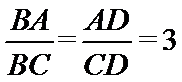
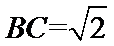
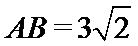
所以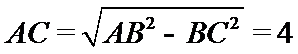
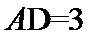
由切割线定理得
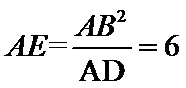
故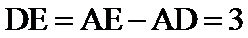
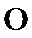
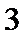
考查方向
解题思路
凡是题目中涉及长度的,通常会使用到相似三角形.全等三角形.正弦定理.余弦定理等基础知识.
易错点
长度计算时几何关系一定要对应好
正确答案
(Ⅰ)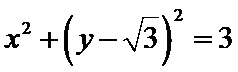
解析
试题分析: (Ⅰ)先将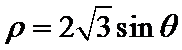
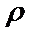
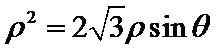
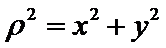
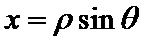
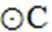
(Ⅰ)由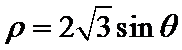
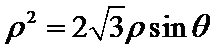
从而有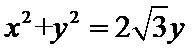
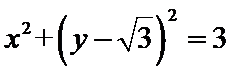
考查方向
解题思路
解决此类问题的关键是极坐标方程或参数方程转化为平面直角坐标系方程
易错点
参数方程与普通方程的转化
正确答案
(Ⅱ)
解析
试题分析:(Ⅱ)先设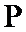
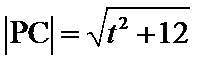
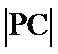
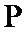
(Ⅱ)设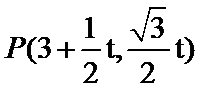
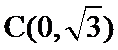
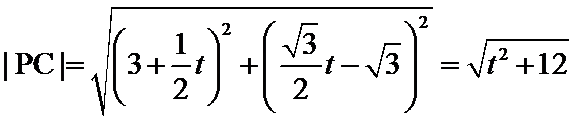
故当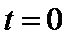
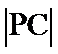
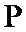
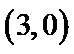
考查方向
解题思路
解决此类问题的关键是根据参数方程参数的几何意义解析分析计算
易错点
参数方程参数的几何意义
正确答案
(Ⅰ)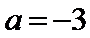
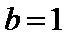
解析
试题分析: (Ⅰ)先由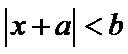
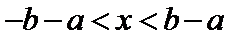
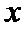
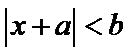
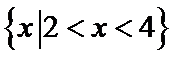
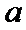
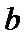
(Ⅰ)由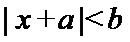
则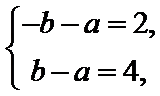
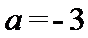
考查方向
解题思路
解题时一定要注意不等式与方程的区别,否则很容易出现错误.零点分段法解绝对值不等式的步骤:①求零点;②划区间,去绝对值号;③分别解去掉绝对值的不等式;④取每段结果的并集,注意在分段时不要遗漏区间的端点值.
易错点
注意不等式与方程的区别
正确答案
(Ⅱ)
解析
试题分析:(Ⅱ)先将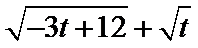
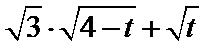
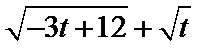
(Ⅱ)
当且仅当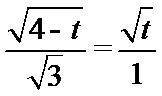
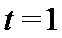
故
考查方向
解题思路
用柯西不等式证明或求最值要注意:①所给不等式的形式是否与柯西不等式的兴致一致,若不一致,需要将所给式子变形;②等号成立的条件.
易错点
不等式性质的灵活运用
15.在平面直角坐标系中,当P(x,y)不是原点时,定义P的“伴随点”为P(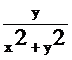
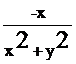
①若点A的“伴随点”是点A′,则点A′的“伴随点”是点A.
②单位圆上的点的“伴随点”仍在单位圆上;
③若两点关于x轴对称,则它们的“伴随点”关于y轴对称;
④若三点在同一条直线上,则它们的“伴随点”一定共线.
其中的真命题是 (写出所有真命题的序号).
正确答案
②③
解析
① 设
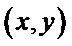
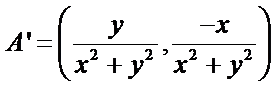
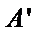
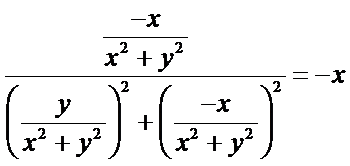
故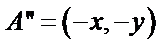
② 设单位圆上的点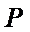
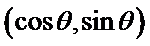
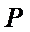
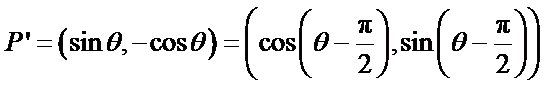
所以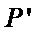
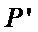
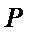
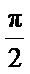
③ 设曲线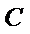
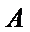
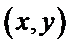
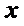
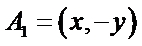
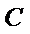
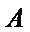
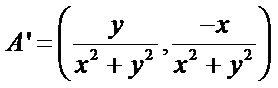
点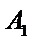
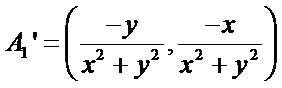
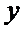
④ 反例:例如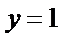
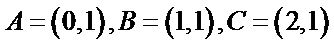
随点分别是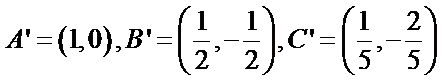
设点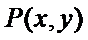
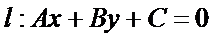

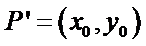
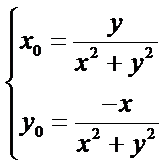
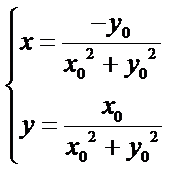
带入直线方程可知: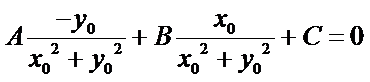
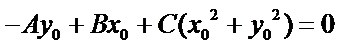
当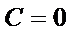
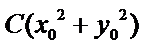
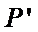
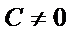
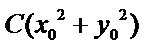
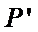
所以,直线“伴随曲线”不一定是一条直线. 错误.
考查方向
解题思路
本题考查了新定义问题与曲线与方程的问题.
易错点
本题考查新定义问题,属于创新题,符合新高考的走向.它考查学生的阅读理解能力,接受新思维的能力。本题容易在理解定义时出错。
知识点
8.方程
正确答案
2
解析
依题意

令



当




当





所以
考查方向
解题思路
对可化为a2x+b·ax+c=0或a2x+b·ax+c≥0(a2x+b·ax+c≤0)的指数方程或不等式,常借助换元法解决.求解与指对数有关的复合方程问题,首先要熟知指对数式的定义域、值域、单调性等相关性质,其次要明确复合的构成,涉及值域、单调区间、最值等问题时,都要借助“同增异减”这一性质分析判断,最终将问题归结为内层方程相关的问题加以解决.
易错点
与对数有关的问题,应注意对数的真数大于零.
知识点
10.已知函数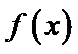
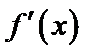
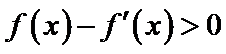
正确答案
解析
设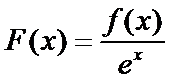
∴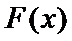
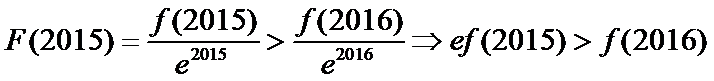
考查方向
解题思路
过
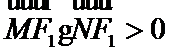
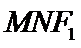
角形,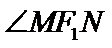
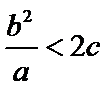
易错点
本题构造函数不正确得不到正确结论。
知识点
16.函数

正确答案
解析
因为







考查方向
解题思路
先求导,再利用基本不等式来求解。
易错点
导数的几何意义不清楚。
知识点
扫码查看完整答案与解析