- 导数的运算
- 共307题
已知函数
(1)若


(2)对于任意的


正确答案
见解析。
解析
(1)

①当




②当


③当




(2)令

令



















又



知识点
设集合


正确答案
解析
略
知识点
甲、乙两个工作室工程师结构如右表:
现因工作需要,要选派2名工程师支援外地建设,每名工程师被选派的机会均等。
(1)若工作室中有一名张姓工程师,求这名工程师被选派的概率;
(2) 求选派的2名工程师都是高级工程师的概率;
(3)求选派的2名工程师属于同一个工作室的概率。
正确答案
见解析。
解析
(1)工作室共有工程师7人,每名工程师被选派的机会均等,
任意选派1人,张姓工程师被选派的概率为
任意选派2人张姓工程师被选派的概率为2×

(2)工作室共有高级工程师3名,依次编号为x1,x2,x3;普通工程师4名,依次编号为y1,y2,y3,y4,
则任意选派两名工程师这一事件所包含的基本事件空间为:
(x1,x2),(x1,x3),(x1,y1),(x1,y2),(x1,y3),(x1,y4),
(x2,x3),(x2,y1),(x2,y2),(x2,y3),(x2,y4),
(x3,y1),(x3,y2),(x3,y3),(x3,y4),
(y1,y2),(y1,y3),(y1,y4),
(y2,y3),(y2,y4),
(y3,y4).共21个基本事件,
其中选派的两名工程师都是高级工程师的基本事件有:
(x1,x2),(x1,x3),(x2,x3)共3个基本事件,其发生概率为
解法一:甲工作室共有工程师3名,依次编号为a1,a2,a3;乙工作室有工程师4名,依次编号为b1,b2,b3,b4,
则任意选派两名工程师这一事件所包含的基本事件空间为:
(a1,a2),(a1,a3),(a1,b1),(a1,b2),(a1,b3),(a1,b4),
(a2,a3),(a2,b1),(a2,b2),(a2,b3),(a2,b4),
(a3,b1),(a3,b2),(a3,b3),(a3,b4),
(b1,b2),(b1,b3),(b1,b4),
(b2,b3),(b2,b4),
(b3,b4).共21个基本事件,
其中选派的两名工程师属于同一个工作室的基本事件有:
(a1,a2),(a1,a3),
(a2,a3),
(b1,b2),(b1,b3),(b1,b4),
(b2,b3),(b2,b4),
(b3,b4)。共9个基本事件,其发生概率为
解法二:甲工作室共有工程师3名,依次编号为a1,a2,a3;乙工作室有工程师4名,依次编号为b1,b2,b3,b4,
则任意选派两名工程师这一事件所包含的基本事件空间为:
(a1,a2),(a1,a3),(a1,b1),(a1,b2),(a1,b3),(a1,b4),
(a2,a3),(a2,b1),(a2,b2),(a2,b3),(a2,b4),
(a3,b1),(a3,b2),(a3,b3),(a3,b4),
(b1,b2),(b1,b3),(b1,b4),
(b2,b3),(b2,b4),
(b3,b4).共21个基本事件,
其中选派的两名工程师属于不同工作室的基本事件有:
(a1,b1),(a1,b2),(a1,b3),(a1,b4),
(a2,b1),(a2,b2),(a2,b3),(a2,b4),
(a3,b1),(a3,b2),(a3,b3),(a3,b4),共12个基本事件,其发生概率为
故选派的两名工程师属于同一个工作室的概率为1
知识点
函数
正确答案
7
解析

当


当


当


当
知识点
在


正确答案
解析
略
知识点
已知


(1)若曲线




(2)设




正确答案
见解析
解析
(1)



依题意有
可得


(2)
不妨设
则

即
设
则对任意的


等价于


可得
依题意有,对任意

由

知识点
已知函数
(1)若函数

(2)设
正确答案
见解析。
解析
(1)
因为

即

当

设

所以当且仅当




所以
(2)





知识点
已知函数
(1)讨论函数
(2)当



正确答案
见解析
解析
(1) 

(i)当




(ii)当

当



当



(iii)当

当




当



综上,当




当


当




(其中
(2)当
令
将


由此表可得

又
故区间



知识点
一个几何体的三视图如右图所示,则该几何体的体积是( )
正确答案
解析
略
知识点
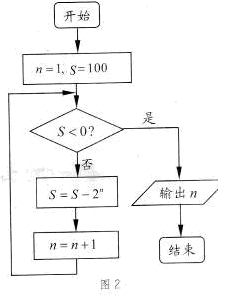
执行如图2所示的程序框图,则输出的n值为
(注:“n=1”,即为“n←1”或为“n:=1”,)
正确答案
解析
略
知识点
扫码查看完整答案与解析