• 职业资格类
  • 建筑类
  • 学历类
  • 财会类
  • 医药类
  • 全部考试
职业资格类
建筑类
学历类
财会类
计算机类
公务员
医药类
  • 平面向量的基本定理及其意义
  • 共28题
  • 平面向量的基本定理及其意义
  • 共28题

热门试卷

X 查看更多试卷
1
题型：填空题
|
填空题 · 5 分

15.已知的重心为O，过O任做一直线分别交边AB，AC于P，Q两点，设，则的最小值是______.

正确答案

解析

如图所示

∵P，O，Q三点共线，则

∵的重心为O

∴

∴

考查方向

本题主要考查了向量的几何意义以及三点共线定理、基本不等式

解题思路

先利用向量的几何意义，利用三点共线，得出的关系，然后利用基本不等式求解

易错点

本题不会利用三点共线转化

知识点

平面向量的基本定理及其意义向量在几何中的应用
1
题型： 单选题
|
单选题 · 5 分

11.在等腰直角中，在边上且满足：，

若，则的值为

A

B

C

D

正确答案

A

解析

∵,

∴A，B，D三点共线，

∴由题意建立如图所示坐标系，

设AC=BC=1，则C(0，0)，A(1，0)，B(0，1)，

直线AB的方程为，

直线CD的方程为

故联立解得，

故

故

,

故,

故，解得，

故选A.

考查方向

本题考查了平面向量坐标运算的应用．

解题思路

易知A，B，D三点共线，从而建立坐标系，从而利用坐标运算求解即可．

易错点

在平面中A、B、C三点共线的充要条件是： (O为平面内任意一点)，其中x+y=1.

知识点

平面向量的基本定理及其意义
1
题型： 单选题
|
单选题 · 5 分

8．O是平面上一定点，A、B、C平面上不共线的三点，动点P满足

                           则P点的轨迹一定经过ABC的（ ）

A外心

BB.内心

CC.重心

DD.垂心

正确答案

B

解析

由已知可得由这个等式可知AP在由AB与AC所在的2个单位向量所组成的棱形的对角线上，即角平分线上，故A正确。

考查方向

本题主要考查单位向量，向量的加减法，三角形的内心。

解题思路

将已知的等式化简，根据向量共线基本定理找到AP是在三角形的角平分线上。

易错点

1、不能根据已知的等式将其化简。

知识点

平面向量的基本定理及其意义
1
题型： 单选题
|
单选题 · 5 分

8. 向量在正方形网格中的位置如图所示，则 （    ）

A

B

C

D

正确答案

C

解析

由图可知，所以

考查方向

本题主要考查向量的基本运算和坐标运算，难度较低，属高考重要考点。向量的运算在高考中常结合三角形考查，主要考察求向量的模、投影、夹角等。

解题思路

把都正交分解，然后用表示，最后再求差,或直接在图中作出，然后再用正交分解把它用表示，还可以去用坐标运算

易错点

在正交分解的时候把某一方向弄反，或在后面作差的时候没有变号

知识点

平面向量的基本定理及其意义
1
题型： 单选题
|
单选题 · 5 分

7. 如图，在6×6的方格纸中，若起点和终点均在格点的向量，，满足，（），则（      ）

A0

B1

C

D

正确答案

D

解析

=（1，2），=（-2，1），=（3，4）.所以x+y=。

A选项不正确，B选项不正确，C选项不正确，所以选D选项。

考查方向

本题主要考查了平面向量的坐标运算,在近几年的各省高考题出现的频率较高。A选项不正确，B选项不正确，C选项不正确，所以选D选项。

解题思路

本题考查平面向量的坐标，解题步骤如下：1、写出、、的坐标。2、由题线性表示即可.

易错点

本题易在应用线性表示时发生错误。

知识点

平面向量的基本定理及其意义
1
题型： 单选题
|
单选题 · 5 分

8．O是平面上一定点，A、B、C平面上不共线的三点，动点P满足

                           则P点的轨迹一定经过ABC的（ ）

A外心

BB.内心

CC.重心

DD.垂心

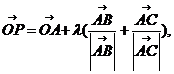
正确答案

B

解析

由已知可得由这个等式可知AP在由AB与AC所在的2个单位向量所组成的棱形的对角线上，即角平分线上，故A正确。

考查方向

本题主要考查单位向量，向量的加减法，三角形的内心。

解题思路

将已知的等式化简，根据向量共线基本定理找到AP是在三角形的角平分线上。

易错点

1、不能根据已知的等式将其化简。

知识点

平面向量的基本定理及其意义向量在几何中的应用
1
题型：简答题
|
多选题

依据《注册安全工程师管理规定》，注册安全工程师实行分类注册，注册类别包括 ( )。

A．煤矿安全
B．非煤矿矿山安全
C．建筑施工安全
D．危险物品安全
E．烟花爆竹安全

正确答案

A,B,C,D

解析

暂无解析

1
题型：填空题
|
填空题 · 5 分

16.   在中，角，，所对边的长分别为，，，为边的中点，

且，又已知，   则角

                            ．

正确答案

解析

因为所以,CM和MP平行，且、可知, 因为又因为，，所以

考查方向

解直角三角形、正弦定理、余弦定理

解题思路

根据给出的向量之间的关系和线段之间的关系，利用余弦定理求解

易错点

向量模和向量平行概念不理解

知识点

向量的线性运算性质及几何意义平面向量的基本定理及其意义
1
题型： 单选题
|
单选题 · 5 分

3． 如图, 正方形中，为的中点，若，则的值为（    ）

A

B

C

D

正确答案

A

解析

因为 ，所以．

考查方向

本题考查了平面向量的三角形法则，在近几年的各省高考题出现的频率较低．

解题思路

利用基向量 将向量 分解．

易错点

使用加法公式 ，或者中点公式将使问题变得复杂．

知识点

平面向量的基本定理及其意义向量在几何中的应用
棒棒哒，已学完当前知识点 学习下一知识点
下一知识点 : 平面向量的坐标运算
百度题库 > 高考 > 文科数学 > 平面向量的基本定理及其意义

扫码查看完整答案与解析

  • 上一题
  • 1/9
  • 下一题