- 由其它方法求数列的通项公式
- 共33题
12.在数列{an}中,a1=3, an=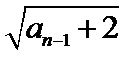
正确答案
解析
由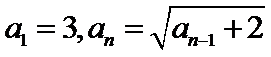
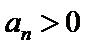
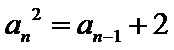
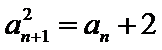
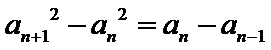
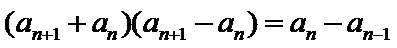
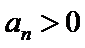
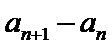
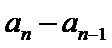
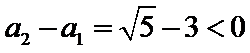
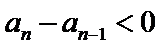
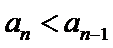
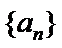
考查方向
解题思路
先对an=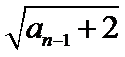
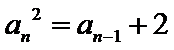
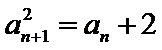
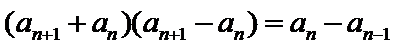
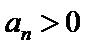
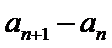
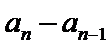
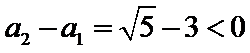
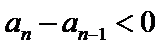
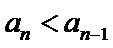
故B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
转化条件an=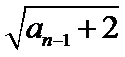
知识点
8. 已知数列{an}的前n项和为Sn ,点(n,Sn)在函数f(x)=
正确答案
考查方向
解题思路
(1)求积分;(2)代入解析式;
易错点
由前n项和求通项时,注意n的限定条件。
知识点
已知数列

24.若

25.若



正确答案
见解析
解析
(1)
当
当
考查方向
解题思路
由数列

易错点
主要易错于递推关系找不出,
正确答案
见解析
解析
(2)方法1:

①/②得,因为
方法2:因为
又因为
所以

所以

所以:
考查方向
解题思路
这里可以从两个方面进行分析
①直接找出
②根据递推关系得出
易错点
主要易错于递推关系找不出,
已知






22.求数列

23.设






正确答案
(1)
解析
(1)因为

所以



所以
考查方向
解题思路
1.第(1)问根据等差数列、等比数列的基本量求出通项公式;2.根据第(1)问求出
易错点
1.不会将


正确答案
(1)
解析
(2)

所以

(或
因为



所以,不存在正整数

考查方向
解题思路
1.第(1)问根据等差数列、等比数列的基本量求出通项公式;2.根据第(1)问求出
易错点
1.不会将


已知


17.求数列
18.求数列


正确答案
(1)
解析
(1) 设



由


考查方向
解题思路
利用等差数列的性质求出数列
易错点
利用等差数列的性质求通项公式和等比数列的性质混淆;
正确答案
解析
(2)
由
得
① -②得

又
当


考查方向
解题思路
根据公式构造等式求出
易错点
先构造等式做差后求出
扫码查看完整答案与解析





















































