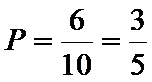- 实际推断原理和假设检验
- 共1题
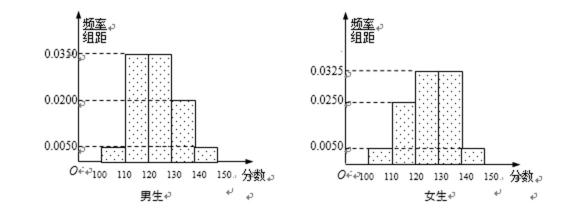
18.某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图.
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,
附:
正确答案
(1)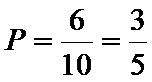
解析
试题分析:本题属古典概型及独立性检验,(1)先根据分层抽样算出抽出的人数,然后利用古典概型的公式计算;(2)列出联表然后代入公式计算出k的观测值,然后下结论。
试题解析:(1)解:由已知得,抽取的100名学生中,男生60名,女生40名
分数小于等于110分的学生中,
男生人有60×0.05 = 3(人),记为A1,A2,A3;女生有40×0.05 = 2
从中随机抽取2名学生,所有的可能结果共有10种,
(A2,A3),(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2)
其中,两名学生恰好为一男一女的可能结果共有6种,它们是:(A1,B1),(A1,B2),
(A2,B1),(A2,B2),(A3,B1),(A3,B2),
故所求的概率
(2)解:由频率分布直方图可知,
在抽取的100名学生中,男生 60×0
据此可得2×2列联表如下:
所以得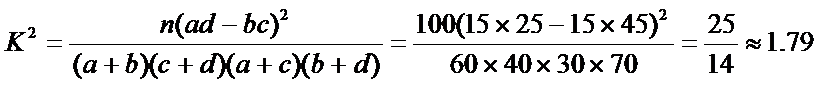
因为1.79 < 2.706.
所以没有90%的把握认为“数学尖子生与性别有关”.
考查方向
解题思路
本题考查了古典概型及独立性检验,解题步骤如下:(1)先根据分层抽样算出抽出的人数,然后利用古典概型的公式计算;(2)列出联表然后代入公式计算出k的观测值,然后下结论。
易错点
在找基本事件的个数的时候有可能遗漏或者重复。
知识点
扫码查看完整答案与解析