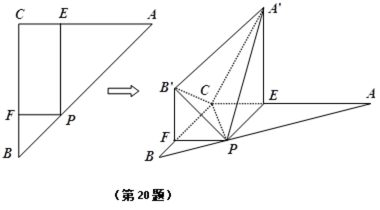平面的概念、画法及表示
共36题

· 平面的概念、画法及表示

平面的概念、画法及表示
共36题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

17.现需要设计一个仓库，它由上下两部分组成，上部的形状是正四棱锥，下部的形状是正四棱柱(如图所示)，并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.

(1) 若AB=6 m,PO1=2 m，则仓库的容积是多少？

(2) 若正四棱锥的侧棱长为6 m,则当为多少时，仓库的容积最大？

正确答案

故仓库的容积为；

(2)

当时，，单调递增，
当时，，单调递减，

因此，当时，取到最大值，
即时，仓库的容积最大．

知识点

平面的概念、画法及表示

题型：简答题

简答题 · 14 分

16．如图，在四棱锥中，底面为矩形，平面平面，，，为的中点，求证：

（Ⅰ）平面；

（Ⅱ）平面平面；

（Ⅲ）求四棱锥的体积.

正确答案

（3）略

解析

解析已在路上飞奔，马上就到！

知识点

平面的概念、画法及表示

题型：单选题

单选题 · 5 分

8．在中，，AD是边BC上的高，则的值等于（）

D-4

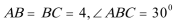
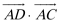
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面的概念、画法及表示

题型：简答题

简答题 · 15 分

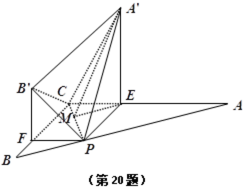
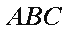
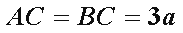
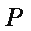
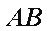
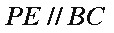
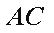
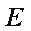
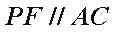
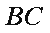
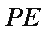
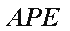
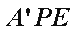
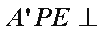
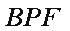
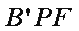
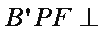
如图，在△中，，，点在上，交于，交于，沿将△翻折成△，使平面平面；沿将△翻折成△，使平面平面。

（1）求证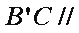：平面；

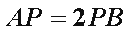
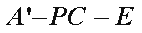
（2）若，求二面角的平面角的正切值。

正确答案

见解析

解析

（1）因为，平面，所以平面。

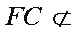
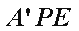
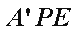
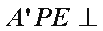
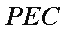
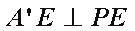
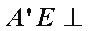
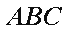
因为平面平面，且，所以平面。

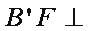
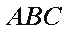
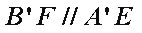
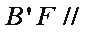
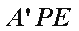
同理，平面，所以，从而平面。

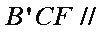
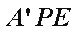
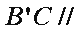
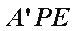
所以平面平面，从而平面。

（2）因为，，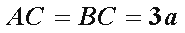

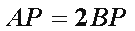
所以，，，。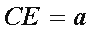

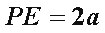
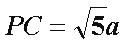
过E作，垂足为M，连结。

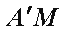
由（1）知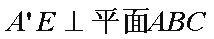，可得，

所以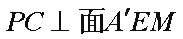，所以。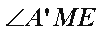

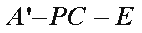
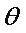
所以即为所求二面角的平面角，可记为。

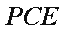
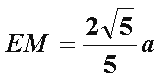
在Rt△中，求得，

所以。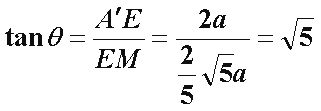

知识点

平面的概念、画法及表示

题型：填空题

填空题 · 5 分

如图，AB是半圆O直径，BAC=30o。BC为半圆的切线，且BC=4，则点O到AC的距离OD= 。

正确答案

解析

试题分析：直角三角形ABC中，BAC=30o，BC=4，所以直角三角形ABC中，BAC=30o ，所以

知识点

平面的概念、画法及表示

继续学习学习下一知识点

下一知识点 : 平面的基本性质及推论

百度题库 > 高考 > 文科数学 > 平面的概念、画法及表示

扫码查看完整答案与解析