四种命题及真假判断
共353题

· 四种命题及真假判断

四种命题及真假判断
共353题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

设命题：函数的图象向左平移单位得到的曲线关于轴对称；

命题：函数在上是增函数，则下列判断错误的是

A为假

B为真

C为假

D为真

正确答案

解析

略

知识点

四种命题及真假判断

题型：简答题

简答题 · 14 分

（1）证明：对，；

（2）数列，若存在常数，，都有，则称数列有上界。已知，试判断数列是否有上界。

正确答案

见解析。

解析

证明与求解：（1）设，。，解得

当时，，单调递增；当时，，单调递减。所以在处取最大值，即，，

（2）数列无上界

，设，，由⑴得，，所以，，，取为任意一个不小于的自然数，则，数列无上界

知识点

四种命题及真假判断

题型：单选题

单选题 · 5 分

下列命题为真命题的是

A若为真命题，则为真命题

B“”是“”的充分不必要条件。

C命题“若，则”的否命题为：“若，则”

D已知命题：，使得，则：，使得

正确答案

解析

略

知识点

四种命题及真假判断

题型：填空题

填空题 · 5 分

已知函数则；

下面三个命题中，所有真命题的序号是（）.

① 函数是偶函数；

② 任取一个不为零的有理数，对恒成立；

③ 存在三个点使得为等边三角形。

正确答案

1； ①②③

解析

略

知识点

四种命题及真假判断

题型：单选题

单选题 · 5 分

下列命题中假命题是（　　）

A∀x＞0，有ln2x+lnx+1＞0

B∃α，β∈R，使cos（α+β）=cosα+cosβ

C“a2＜b2”是“a＜b”的必要不充分条件

正确答案

解析

对于A，令lnx=t则ln2x+lnx+1=t2+t+1，因为△=﹣3＜0，所以t2+t+1＞0，所以ln2x+lnx+1＞0，所以A正确；

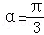
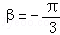
对于B，当，时，有cos（α+β）=cosα+cosβ，所以∃α，β∈R，使cos（α+β）=cosα+cosβ，所以B正确；

对于C，例如a=﹣2，b=1满足“a＜b”推不出“a2＜b2”，所以“a2＜b2”不是“a＜b”的必要不充分条件，所以C不正确；

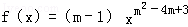
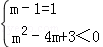
对于D，使是幂函数，且在（0，+∞）上递减，需要所以m=2，所以D正确

故选C

知识点

四种命题及真假判断

继续学习学习下一知识点

下一知识点 : 充分条件

百度题库 > 高考 > 文科数学 > 四种命题及真假判断

扫码查看完整答案与解析